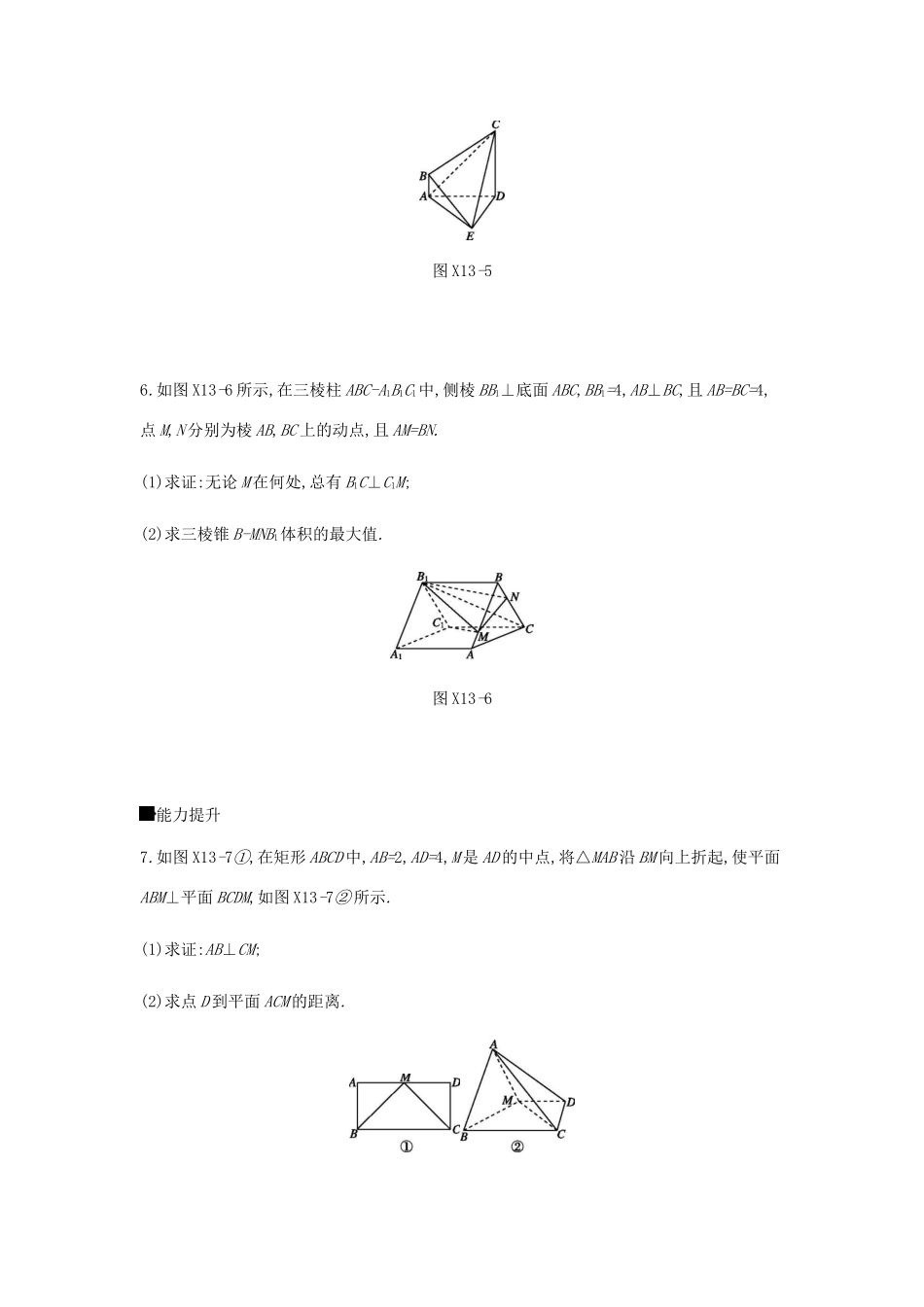
限时集训(十三)立体几何基础过关1.如图X13-1,在底面为正方形的四棱锥P-ABCD中,PA⊥平面ABCD,AC与BD交于点E,点F是PD的中点.(1)求证:EF∥平面PBC;(2)若PA=2AB=2,求点F到平面PBC的距离.图X13-12.如图X13-2,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.(1)证明:平面AEF⊥平面ACC1A1;(2)若AB=EC=2,求三棱锥C-AEF的体积.图X13-23.如图X13-3,在四面体ABCD中,BA=BC,∠BAD=∠BCD=90°.(1)证明:BD⊥AC;(2)若∠ABD=60°,BA=2,四面体ABCD的体积为2,证明:平面BAD⊥平面BCD.图X13-34.如图X13-4,四边形ABCD是菱形,AF⊥BD,AF∥CE,且AF=2CE.(1)求证:平面ACEF⊥平面BDE;(2)已知在线段BF上有一点P,满足AP∥DE,求BPFP的值.图X13-45.如图X13-5,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.(1)求证:平面ACE⊥平面CDE.(2)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出EFED的值;若不存在,说明理由.图X13-56.如图X13-6所示,在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面ABC,BB1=4,AB⊥BC,且AB=BC=4,点M,N分别为棱AB,BC上的动点,且AM=BN.(1)求证:无论M在何处,总有B1C⊥C1M;(2)求三棱锥B-MNB1体积的最大值.图X13-6能力提升7.如图X13-7①,在矩形ABCD中,AB=2,AD=4,M是AD的中点,将△MAB沿BM向上折起,使平面ABM⊥平面BCDM,如图X13-7②所示.(1)求证:AB⊥CM;(2)求点D到平面ACM的距离.图X13-78.如图X13-8,正方体ABCD-A1B1C1D1的棱长为2,E,F分别是CB,CD的中点,点M在棱CC1上,CM=tCC1(0