安徽省和县一中高三数学上学期第一次检测试卷 文试卷VIP免费

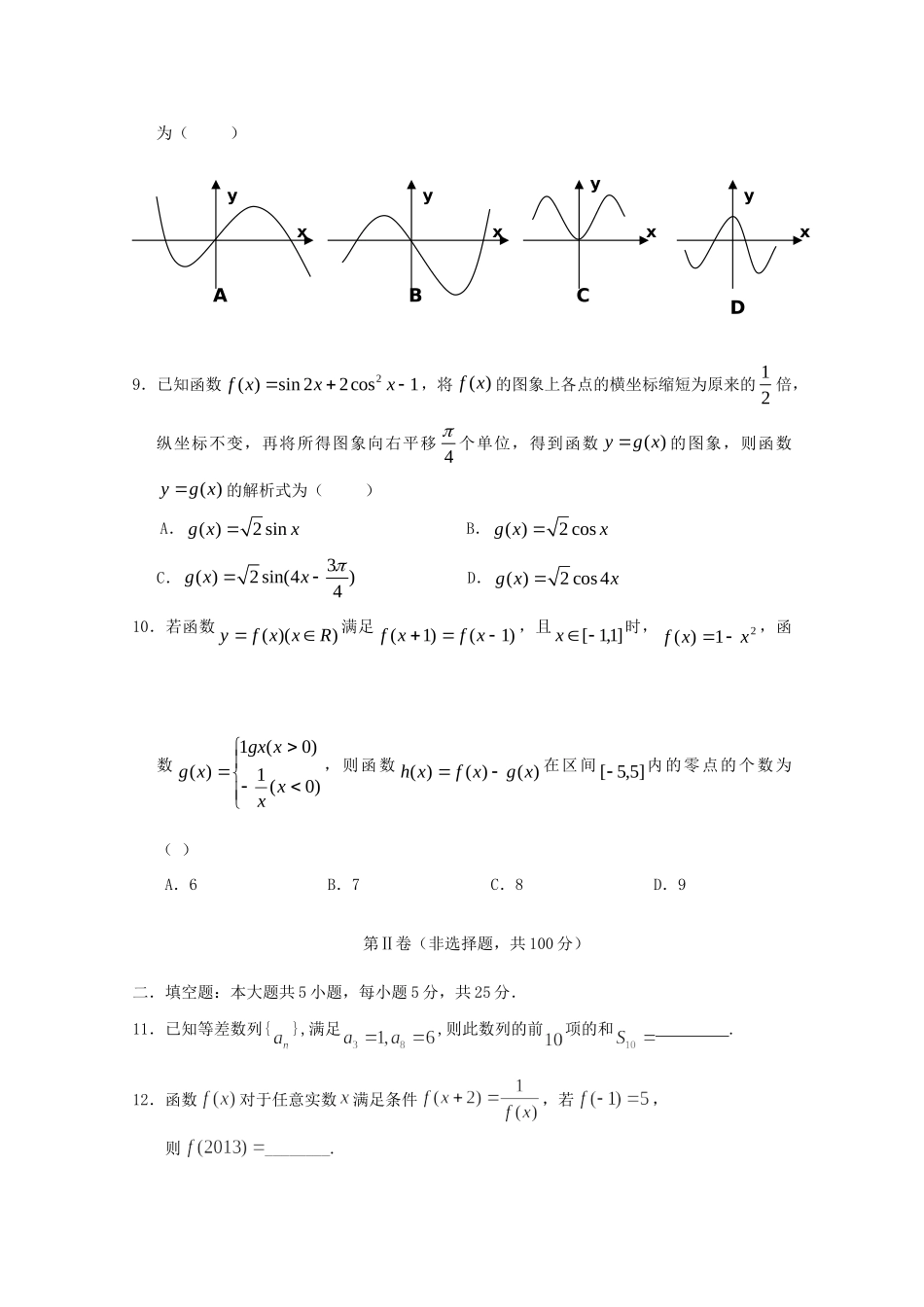
和县一中2015届高三第一次周测数学（文）试卷总分150分考试时间120分钟第Ⅰ卷（选择题，共50分）一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．函数的定义域为（）A．B．C．D．2.已知集合|3Mxx，2|680Nxxx，则MN（）A．B．|03xxC．|13xxD．|23xx3．已知向量，，，若（），则k（）A．2B．2C．8D．84．函数f(x)＝(x－3)ex的单调递增区间是（）A．(－∞，2)B．(0,3)C．(1,4)D．(2，＋∞)5．已知函数f(x)＝x3－2ax2－3x(a∈R)，若函数f(x)的图像上点P(1，m)处的切线方程为3x－y＋b＝0，则m的值为（）A．－B．－C．D．6．()tansin1fxxx，若2)(bf，则)(bf（）A．0B．3C．-1D．-27．已知等比数列的首项公比，则（）A．50B．35C．55D．468．设曲线y＝sinx上任一点(x，y)处切线的斜率为g(x)，则函数y＝x2g(x)的部分图像可以为（）9．已知函数2()sin22cos1fxxx，将()fx的图象上各点的横坐标缩短为原来的12倍，纵坐标不变，再将所得图象向右平移4个单位，得到函数()ygx的图象，则函数()ygx的解析式为（）A．()2singxxB．()2cosgxxC．3()2sin(4)4gxxD．()2cos4gxx10．若函数))((Rxxfy满足)1()1(xfxf，且]1,1[x时，21)(xxf，函数)0(1)0(1)(xxxgxxg，则函数)()()(xgxfxh在区间]5,5[内的零点的个数为（）A．6B．7C．8D．9第Ⅱ卷（非选择题，共100分）二．填空题：本大题共5小题，每小题5分，共25分．11．已知等差数列{},满足,则此数列的前项的和.12．函数对于任意实数满足条件，若，则________.yxAyxBxCxDyy13．函数f(x)＝excosx的图像在点(0，f(0))处的切线的倾斜角为14．在ABC中，角CBA、、所对的边分别为cba、、满足bcacb222，0BCAB,23a,则cb的取值范围是.15．定义两个平面向量的一种运算，则关于平面向量上述运算的以下结论中，①，②，③若，则，④若且则.恒成立的有.(填序号)三、解答题：本大题有6小题，共75分,解答应写出文字说明、证明过程或演算步骤.16.(12分)设命题p：函数f(x)＝lg(ax2－4x＋a)的定义域为R；命题q：不等式对∀x∈(0，+∞1)恒成立．如果命题“p∨q”为真命题，命题“p∧q”为假命题，求实数a的取值范围．17.（满分12分）已知函数()sin(2)(0π)fxx的图像经过点π(,1)12．（1）求的值；（2）在ABC中，A、B、C所对的边分别为a、b、c，若222abcab且π2()2122Af．求sinB．18.(12分)我省某景区为提高经济效益，现对某一景点进行改造升级，从而扩大内需，提高旅游增加值，经过市场调查，旅游增加值y万元与投入)10(xx万元之间满足：baxbxaxxfy,,10ln50101)(2为常数。当10x万元时，2.19y万元；当20x万元时，7.35y万元。（参考数据：6.15ln,1.13ln,7.02ln）（1）求)(xf的解析式；（2）求该景点改造升级后旅游利润)(xT的最大值。（利润＝旅游增加值－投入）。19.（13分）在锐角中，、、所对的边分别为、、．已知向量，，且.（1）求角的大小；（2）若，，求的面积．20.（13分）已知函数.（1）若函数的图象在处的切线斜率为，求实数的值；（2）在（1）的条件下，求函数的单调区间；（3）若函数在上是减函数，求实数的取值范围.21.（13分）已知数列的前项和，满足：.（Ⅰ）求数列的通项；（Ⅱ）若数列的满足，为数列的前项和，求证：.