高中数学思想讲座 数学方法的优美 新课标 人教版 课件VIP免费

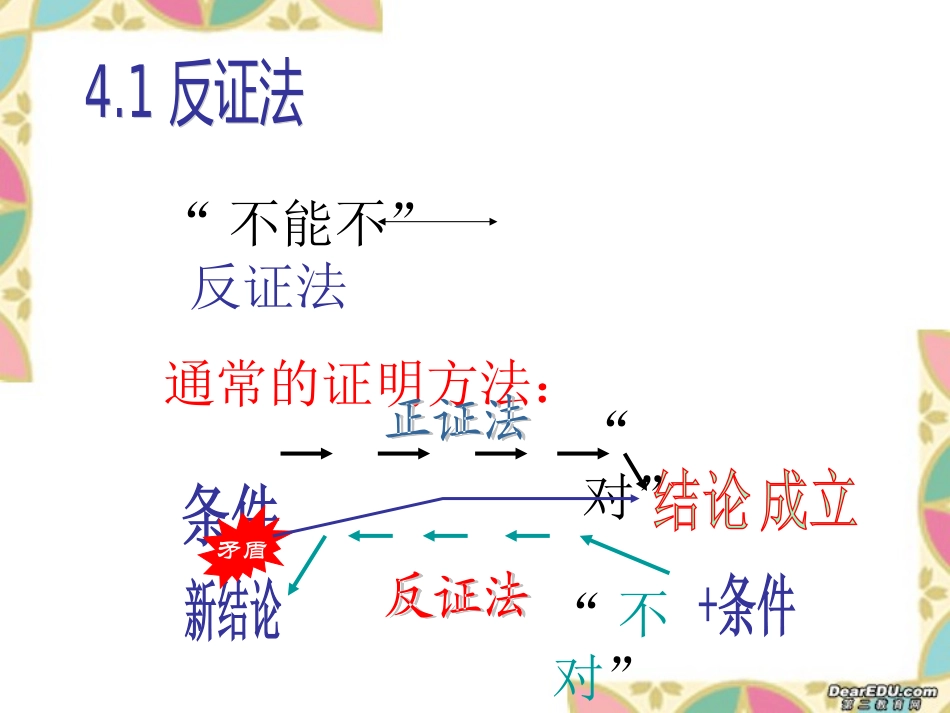
观点和方法是数学的两个方面：既紧密联系，又有所区别。但方法影响观点。我们来看看数学方法的美。“不能不”反证法通常的证明方法：“对”“不对”矛盾例12.是无理数反证法：2,,,pq不假设是有理数那么存在的正整数可约使得2222.qpqqp为偶数222,2,..qmpmp设则于是为偶数矛盾也177.是有理数至多步就可以找到规律例2（抽屉原理）3个苹果放进2个抽屉中，至少有1个抽屉中有两个苹果。（反证法易得）10本书，共3类（抽屉），文学类（A）、史学类（B）和数学类（C），证明至少有一类有4本或4本以上。10本书，共3类（抽屉），文学类（x）、史学类（y）和数学类（z），证明x,y,z至少有一个大于或等于4。抽象为一个纯数学问题：,,10,4,4,4.xyzxyzxyz假设是非负整数,且则或或或此即为不定方程的非负解的下界估计问题.假设人类的头发最多为200万根，那么长春市至少有2人的头发根数一样多。（长春市人口超过200万）作业：在任意6人中，一定可以找到3个相互认识，或3个相互不认识的人。RMI：R-relation,M-mapping,I-inversion.即关系、映射和取逆。它属于形式逻辑范畴。如“三段式”给人以逻辑美。RMI方法体现了辨证思想的方法。例111101134422221024204822228161682562048显得容易。例21112?等于多少11110.3010,lg2lg20.02731111很难但是11:21.065.从反对数表得到lg1lg0xxxx运算数值曲折：化难为易曲折：创造、发明曲折：实现的根据是对数Galileo：给我空间、时间和对数，我即可创造一个宇宙。RMI的体现：R：21/11，M：lgx,I:10lgx例3:求和11111(1)35721nyn35721()(1)35721nnxxxxyxxnRM,逐项微分246221'()1(1)1nnyxxxxxx201()arctan,(1).14xyxdxxyyxI,积分数学上互逆的运算很多:如0的作用是+项与-项;1的作用是乘项与除项.抽象=枯燥乏味?语言学抽象吗?美、神、好文学抽象吗？诗歌艺术抽象吗？绘画、舞蹈音乐抽象吗？高山流水、悲欢离和数学的抽象美的表现形式不同，它给人带来的是简洁、明快和高效的美例1（七桥问题）如图，能否从某个桥出发，走过所有的桥，但每座桥只经过一次？ABCD？？BACDBACD24213313335点线图——拓扑学topology:不注重数量关系和形状特征，而注重点与点的连接方式！如：建立校园网络系统。从网络中心到各办公楼、教学楼、学生宿舍楼，到各办公室、教室和寝室。你任何设计呢？你需要建立一个网络的拓扑图即可。实际上如果两个图的点与连接方式一致，它们实际上就是拓扑意义下的一张图。拓扑学的产生与发展进一步表现了数学的抽象程度，起抽象的美与实际是如此的协调，展示了数学的优美！拓扑学的产生极大冲击了直观性原则！1人的认知能力(直观，抽象飞跃)2直观与抽象在认识上的统一受年龄和知识的接受方式的限制.3直观可能造成错觉.思辩的作用越来越大.直观具有较大的局限性.物理学、化学、生物学等学科中许多重大发现和突破是有想象力开导的。善于抽象不仅只限于数学，人文科学、社会科学，更越来越抽象，只不过给人的感觉不象数学强烈而已。