高三数学 2.4 等比数列2课件 新人教A版必修5 课件VIP免费

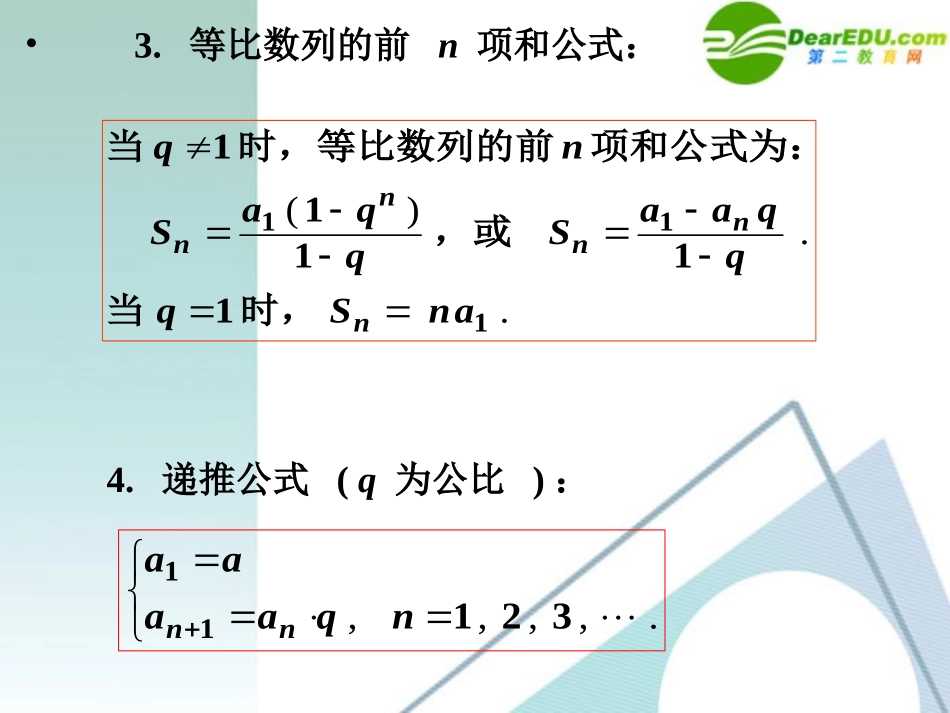
等比数列小结•1.等比数列的定义：定义：如果一个数列从第2项起，每一项与它的前一项的比都等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母q来表示.2.等比数列的通项公式：等比数列的通项公式：an=a1qn–1.•3.等比数列的前n项和公式：..)(11111111anSqqqaaSqqaSnqnnnnn时，当，或项和公式为：时，等比数列的前当4.递推公式(q为公比)：.,,,,32111nqaaaann•5.等比中项：.)(,,0xyxyGyxGyGx的等比中项，且与叫做就成等比数列，那么把定义：若6.等比数列的一条性质：分别与首末两项等距离的两项的积等于首末两项的积.对任意m，n，p，qN*，当m+n=p+q时，有am·an=ap·aq.7.{an}为等比数列的两个充要条件：;,,,,;,,,,32132102211naaanqaannnnn其中②其中①.,,,,.,,,.2338qaqaqqaqaaqaqa注意这里公比是分别为并知其积时，可设它们当四个数成等比数列，这样便于求解它们分别为并知其积时，可设当三个数成等比数列，例1在等比数列{an}中，a1=2，a7a8=80,求a14.解：因为{an}为等比数列，所以a1a14=a7a8..4028018714aaaa•例2已知数列{an}为等比数列，•（1）若m，n，p成等差数列，求证am，an，ap成等比数列.•（2）若a3=-2，a6=54，求a9.证明：（1）由所给条件，可得n–m=p-n.,mnmnmnqqaqaaa1111.npnpnpqqaqaaa1111.npmnaaaa所以，am，an，ap成等比数列.（2）由上题结论，a3，a6，a9成等比数列..145825423269aaa•注：（1）我们可以把例2（1）推广成下面的结论：在一个等比数列中，项数成等差数列的各项所形成的数列仍然是等比数列.（2）由例2的证明过程，我们不难发现下述列论：.;*,,}{mnmnmnmnnqaaqaaNnmaq②①则中，若的等比数列在公比为做题时这两个公式可以直接运用，第二个公式可以看作是等比数列通项公式的一种推广..3101521,,10101010351525150的积仍然在这个数列中）这个数列中任意两项（；项的项是它后面第）这个数列中的任意一（；这个数列是等比数列）（求证：，，，，已知无穷数列例n.)(常数）因为证明：（5151511010101nnnnaa所以，这个数列是等比数列..)(1011010101021545154515nnnnnnaa.1015项的是它后面第这个数列中的任意一项.)()(51151515151101010103qpqpqpqpaa因为p，qN*，所以p+q–1N*,.)(项数列的第是，是这个数列中的一项110511qpaaqpqp•例4设某个等比数列前4项的和为2，前8项的和为8，求前12项的和.解：设此数列的首项为a1，公比为q，若q=1，则4a1=2，8a1=8，此二式是矛盾的，故q1.)()()()(281112118141qqaqqa于是.,11314qaq解得.)(])([)()(2631111133412112qqqaS•解法二：因为•a1+a2+a3+a4=a1+a1q+a1q2+a1q3,•a5+a6+a7+a8=a1q4+a1q5+a1q6+a1q7,•a9+a10+a11+a12=a1q8+a1q9+a1q10+a1q11.48812448SSSSSSS把S4=2，S8=8代入上式，即可求得S12=26.,48765121110943218765qaaaaaaaaaaaaaaaa注：由本例解法二我们可以发现等比数列的又一条性质：把等比数列从第一项起依次每相同数目的项相加所得到的数列仍然是等比数列.•练习题：.,,)(.,,)(.,,,}{qSaaaaqnSaaannn求已知求已知和公比求）已知（为等比数列，已知6238129409131336931.)(;)(;,211322231416qqaqn或）答案：（