高中数学(圆锥曲线综合)课件 新人教版选修2-1 课件VIP免费

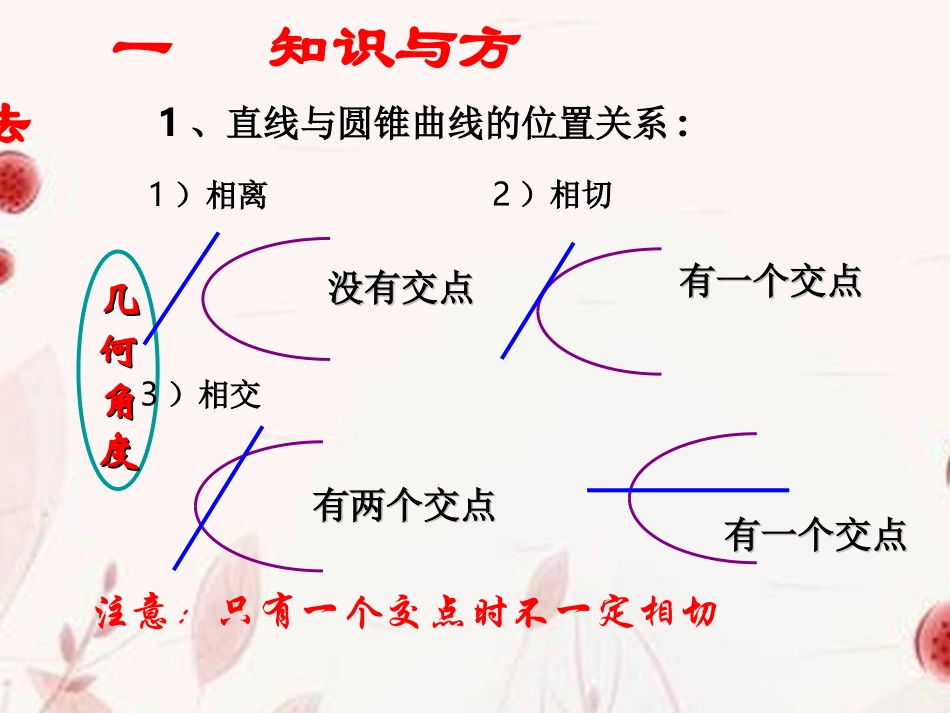
圆锥曲线综合（二）一知识与方法1、直线与圆锥曲线的位置关系:几几何何角角度度有两个交点有两个交点没有交点没有交点有一个交点有一个交点1）相离2）相切3）相交有一个交点有一个交点注意：只有一个交点时不一定相切判断直线l与圆锥曲线C的位置关系时，可将直线l的方程代入曲线C的方程，消去y(或x)得一个关于变量x(或y)的一元二次方程ax2+bx+c=0（或ay2+by+c=0）.(1)若a≠0，Δ＝b2－4ac，则①Δ>0，直线l与圆锥曲线有交点．②Δ＝0，直线l与圆锥曲线有公共点．③Δ<0，直线l与圆锥曲线公共点．(2)若a＝0，此时圆锥曲线不是________;当圆锥曲线为双曲线时，l与双曲线的渐近线______；当圆锥曲线为抛物线时，l与抛物线的对称轴______________．平行或重合一无两平行或重合椭圆代数角度代数角度2.弦：直线被圆锥曲线截得的线段称为圆锥曲线的弦。焦点弦：若弦过圆锥曲线的焦点叫焦点弦；通径：若焦点弦垂直于焦点所在的圆锥曲线的对称轴，此时焦点弦也叫通径。=3．设直线Ax＋By＋C＝0与圆锥曲线f(x，y)＝0相交于A(x1，y1)，B(x2，y2)，则弦长|AB|＝1＋k2|x1－x2|＝(1＋k2)[(x1＋x2)2－4x1x2]＝1＋1k2|y1－y2|＝(1＋1k2)[(y1＋y2)2－4y1y2].4、弦的中点问题设A(x1，y1)，B(x2，y2)是椭圆x2a2＋y2b2＝1上不同的两点，且x1≠x2，x1＋x2≠0，M(x0，y0)为AB的中点，则x21a2＋y21b2＝1，x22a2＋y22b2＝1.两式相减可得y1－y2x1－x2·y1＋y2x1＋x2＝－b2a2，22ABOMbkka类似可得为双曲线x2a2－y2b2＝1时，有22ABOMbkka.为抛物线y2＝2px(p＞0)时，有12()2ABkyyp.友情提示：一种方法_-----点差法：在求解圆锥曲线并且题目中交代直线与圆锥曲线相交和被截的线段的中点坐标时，设出直线和圆锥曲线的两个交点坐标，代入圆锥曲线的方程并作差，从而求出直线的斜率，然后利用中点求出直线方程．“点差法”的常见题型有：求中点弦方程、求(过定点、平行弦)弦中点轨迹、垂直平分线问题．必须提醒的是“点差法”具有不等价性，即要考虑判别式Δ是否为正数．一条规律：“联立方程求交点，根与系数的关系求弦长，根的分布找范围，曲线定义不能忘”．xy0AADxy01.直线y=kx-k+1与椭圆的位置关系为()(A)相交(B)相切(C)相离(D)不确定2.已知双曲线方程x2-y2=1，过P(0，1)点的直线l与双曲线只有一个公共点，则l的条数为()(A)4(B)3(C)2(D)13.过点(0，1)与抛物线y2=2px(p＞0)只有一个公共点的直线条数是()(A)0(B)1(C)2(D)314922yx典型例题例3、（1）已知双曲线E的中心为原点，F(3,0)是E的焦点，过F的直线l与E相交于A，B两点，且AB的中点为N(－12，－15)，则E的方程为()．A.x23－y26＝1B.x24－y25＝1C.x26－y23＝1D.x25－y24＝1解析设双曲线的标准方程为x2a2－y2b2＝1(a＞0，b＞0)，由题意知c＝3，a2＋b2＝9，设A(x1，y1)，B(x2，y2)，则有：x21a2－y21b2＝1，x22a2－y22b2＝1，两式作差得：y1－y2x1－x2＝b2x1＋x2a2y1＋y2＝－12b2－15a2＝4b25a2，又AB的斜率是－15－0－12－3＝1，所以将4b2＝5a2代入a2＋b2＝9得a2＝4，b2＝5，所以双曲线的标准方程是x24－y25＝1.答案B∵|AB|＝22，∴a＋b－aba＋b＝1.①设C(x，y)，则x＝x1＋x22＝ba＋b，y＝1－x＝aa＋b，∵OC的斜率为22，∴ab＝22.代入①，得a＝13，b＝23.∴椭圆方程为x23＋23y2＝1.例4、若直线L与椭圆C：x23＋y2＝1交于A、B两点，坐标原点O到直线L的距离为32，求△AOB面积的最大值．[分析]联立直线和椭圆方程，利用根与系数关系后代入弦长公式，利用基本不等式求出弦长的最大值即可．此时3313.224S22221||(1)()ABkxx2(1)k直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查，一直是高考考查的重点，特别是焦点弦和中点弦等问题，涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法，也是考查数学思想方法的热点题型．