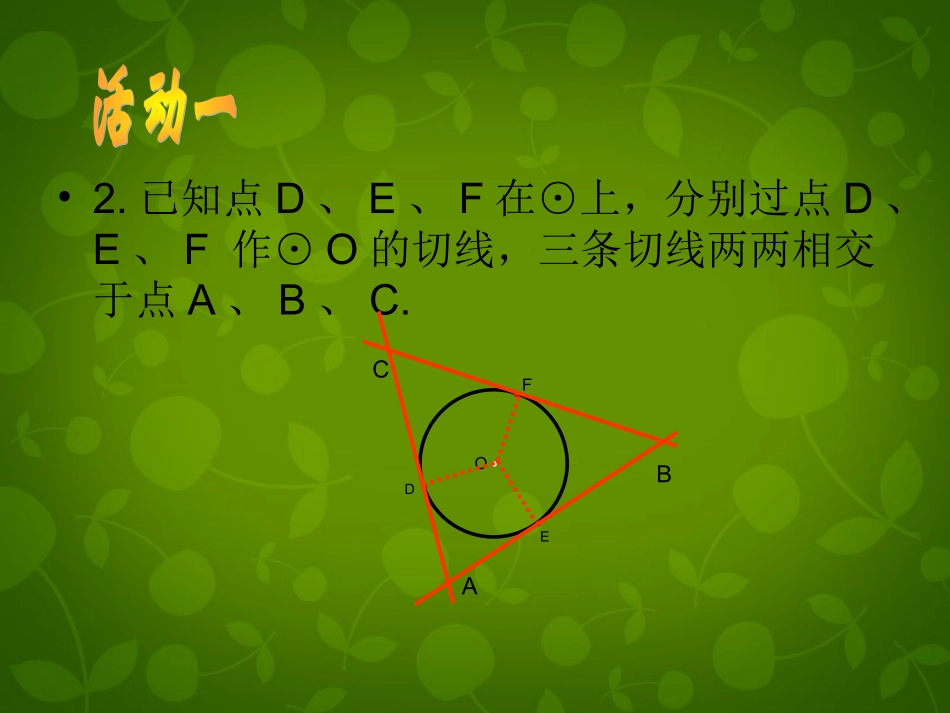
•1.点P在⊙上,过点P作⊙O的切线。OP•2.已知点D、E、F在⊙上,分别过点D、E、F作⊙O的切线,三条切线两两相交于点A、B、C.OFDEABC李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。下图是他的几种设计,请同学们帮他确定一下。ABC作圆:使它和已知三角形的各边都相切已知:△ABC求作:⊙O,使它与△ABC的各边都相切ABCOMND则⊙O就是所求的圆。作法:1、作∠B,∠C的平分线BM和CN,交点为O;2、过点O作ODBC,垂足为D;3、以O为圆心,OD为半径作圆O。类似地,和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形。概念:与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。OBCA想一想:根据作法,与三角形各边都相切的圆能作出几个?为什么?11、什么是三角形的外接圆与内切圆?、什么是三角形的外接圆与内切圆?22、如何画出一个三角形的外接圆与内切圆?、如何画出一个三角形的外接圆与内切圆?画圆的关键:画圆的关键:11、确定圆心、确定圆心22、确定半径、确定半径三角形的外接圆的三角形的外接圆的圆心圆心是各边垂直平分线的交点;是各边垂直平分线的交点;其其半径半径是交点到顶点的距离。是交点到顶点的距离。三角形的内切圆的三角形的内切圆的圆心圆心是各内角平分线的交点;其是各内角平分线的交点;其半径半径是交点到一边的距离。是交点到一边的距离。三角形的外接圆与内切圆的比较三角形的外接圆与内切圆的比较①①经过三角形各顶点的圆叫三角形的经过三角形各顶点的圆叫三角形的外接圆外接圆。。②与三角形各边都相切的圆叫三角形的②与三角形各边都相切的圆叫三角形的内切圆内切圆。。定义:和多边形各边都相切的圆叫做,这个多边形叫做。多边形的内切圆圆的外切多边形内切外切如上图,四边形DEFG是⊙O的四边形,⊙O是四边形DEFG的圆.DEFG.O思考:我们所学的平行四边形,矩形,菱形,正方形,等腰梯形中,哪些四边形一定有内切圆?(菱形,正方形一定有内切圆)定义定义外心(三角形外接圆的圆心)名称确定方法图形性质内心(三角形内切圆的圆心)ABCO三角形三边中垂线的交点ABCO(1)OA=OB=OC;(2)外心不一定在三角形的内部.三角形三条角平分线的交点(1)到三边的距离相等;(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;(3)内心在三角形内部.1、如图1,△ABC是⊙O的三角形。⊙O是△ABC的圆,点O叫△ABC的,它是三角形_________的交点。外接内接外心三边中垂线13、如图2,△DEF是⊙I的三角形,⊙I是△DEF的圆,点I是△DEF的_____心,它是________的交点。2、定义:和三角形各边都相切的圆叫做,内切圆的圆心叫做三角形的,这个三角形叫做____________ABCO.图1IDEF.图2三角形的内切圆内心圆的外切三角形外切内切内角平分线判断题:1、三角形的内心到三角形各个顶点的距离相等()2、三角形的外心到三角形各边的距离相等()3、等边三角形的内心和外心重合;()4、三角形的内心一定在三角形的内部()错错对对例1.在△ABC中,内切圆O与边BC、CA、AB分别相切于点D、E、F,∠B=60度,∠C=70度,求∠EDF的度数OAFEDCB如果∠A=90°,∠BOC=°如果∠A=120°,∠BOC=°如图,在△ABC中,∠A=60°,点O是内心,求∠BOC的度数.OBCA试一试因此:在△ABC中,∠A=n°,点O是△ABC的内心,∠BOC=1351501290°+n°例例22已知:点已知:点II是△是△ABCABC的内心,的内心,AIAI交交BCBC于于DD,交外接圆于,交外接圆于EE。求证:。求证:EB=EI=ECEB=EI=ECAABBCCIIDDEE证明:连结证明:连结BIBI II△是△是ABCABC的内心的内心∴∠∴∠3=4,∠3=4,∠1=2∠∠1=2∠∠,, ∠∠1=2∠1=2∠∴∴∴∴∠∠1=5,∠1=5,∠EB=ECEB=EC∴∠∴∠1+3=4+5∠∠∠1+3=4+5∠∠∠∴∠∴∠BIE=IBE∠BIE=IBE∠∴∴EB=EIEB=EI 又 又EB=ECEB=EC∴∴EB=EI=ECEB=EI=EC1122334455BE=ECCCAABBRRrrOODD例例33求等边三角形的内切圆半径求等边三角形的内切圆半径rr与与外接圆半径外接圆半径RR的比的比..解:由等腰三角形底边解:由等腰三角形底边上的中垂线与顶角平分...