高中数学(三角函数的图像和性质)课件1 湘教版必修2 课件VIP免费

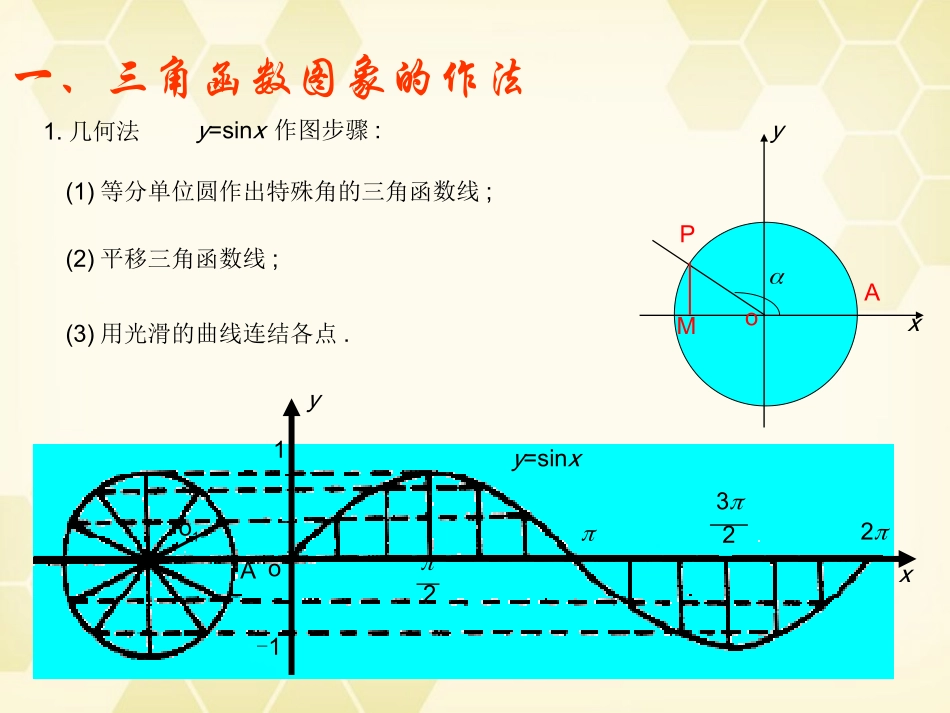
一、三角函数图象的作法1.几何法y=sinx作图步骤:(2)平移三角函数线;(3)用光滑的曲线连结各点.(1)等分单位圆作出特殊角的三角函数线;xyoPMAxyoy=sinx-11o1A22322.五点法作函数y=Asin(x+)的图象的步骤:(1)令相位x+=0,,,,2,解出相应的x的值;232(3)用光滑的曲线连结(2)中五点.(2)求(1)中x对应的y的值,并描出相应五点;3.变换法:函数y=Asin(x+)+k与y=sinx图象间的关系:①函数y=sinx的图象纵坐标不变,横坐标向左(>0)或向右(<0)平移||个单位得y=sin(x+)的图象;②函数y=sin(x+)图象的纵坐标不变,横坐标变为原来的,得到函数y=sin(x+)的图象;1③函数y=sin(x+)图象的横坐标不变,纵坐标变为原来的A倍,得到函数y=Asin(x+)的图象;④函数y=Asin(x+)图象的横坐标不变,纵坐标向上(k>0)或向下(k<0)平移|k|个单位得y=Asin(x+)+k的图象.要特别注意,若由y=sin(x)得到y=sin(x+)的图象,则向左或向右平移应平移||个单位.二、三角函数图象的性质注正切函数的对称中心有两类:一类是图象与x轴的交点,另一类是渐近线与x轴的交点,但无对称轴,这是与正弦、余弦函数的不同之处.1.正弦函数y=sinx(xR)是奇函数,对称中心是(k,0)(kZ),对称轴是直线x=k+(kZ);余弦函数y=cosx(xR)是偶函数,对称中心是(k+,0)(kZ),对称轴是直线x=k(kZ)(正,余弦函数的对称轴为过最高点或最低点且垂直于x轴的直线,对称中心为图象与x轴的交点).222.正切函数y=tanx(xR,x+k,kZ)是奇函数,对称中心是(,0)(kZ).2k2三、正、余弦函数的性质1.定义域:都是R.2.值域:都是[-1,1].对y=sinx,当x=2k+(kZ)时,y取最大值1;当x=2k+(kZ)时,y取最小值-1;对y=cosx,当x=2k(kZ)时,y取最大值1,当x=2k+(kZ)时,y取最小值-1.2233.周期性:①y=sinx、y=cosx的最小正周期都是2;②f(x)=Asin(x+)和f(x)=Acos(x+)的最小正周期都是T=.||24.奇偶性与对称性:正弦函数y=sinx(xR)是奇函数,对称中心是(k,0)(kZ),对称轴是直线x=k+(kZ);余弦函数y=cosx(xR)是偶函数,对称中心是(k+,0)(kZ),对称轴是直线x=k(kZ)(正(余)弦型函数的对称轴为过最高点或最低点且垂直于x轴的直线,对称中心为图象与x轴的交点).225.单调性:y=sinx在[2k-,2k+](kZ)上单调递增,在[2k+,2k+](kZ)上单调递减;y=cosx在[2k,2k+](kZ)上单调递减,在[2k+,2k+2](kZ)上单调递增.222232.值域是R,在上面定义域上无最大值也无最小值.1.定义域:{x|x+k,kZ}.23.周期性:是周期函数且周期是,它与直线y=a的两个相邻交点之间的距离是一个周期.注一般说来,某一周期函数解析式加绝对值或平方,其周期性是:弦减半、切不变.四、正切函数的性质oxy五、典型例题例1利用单位圆中的三角函数线证明当0<<时,不等式sin<cosx.{x|+2k