高一数学 面面垂直的判定课件VIP免费

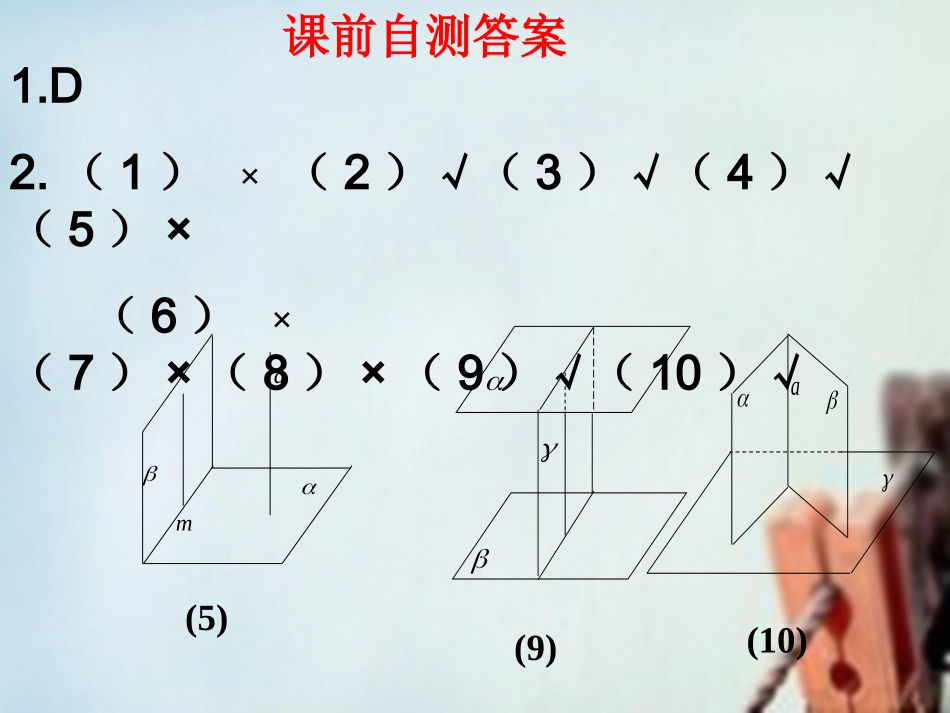
ama1.D2.（1）×（2）√（3）√（4）√（5）×（6）×（7）×（8）×（9）√（10）√课前自测答案(10)(9)(5)1.2.3平面与平面垂直1、两个平面垂直的定义记作：αβ⊥如果两个相交平面的交线与第三个平面垂直，又这两个平面与第三个平面相交所得的交线互相垂直，就称这两个平面互相垂直。ABEDC,BACDBECDABBE建筑工人砌墙时，常用一端系有铅锤的线来检查所砌的墙面是否和地面垂直。如果系有铅锤的线和墙面紧贴，那么所砌的墙面与地面垂直。引入大家知道其中的理论根据吗？符号:αβaA简记：线面垂直，则面面垂直面面垂直线面垂直线线垂直aa面符号:2、两个平面垂直的判定定理：如果一个平面过另一个平面的一条垂线，则两个平面互相垂直。3、两个平面垂直的性质定理如图2，α⊥β，α∩β=CD，AB⊂α，ABCD⊥，求证：AB⊥β.如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面．ABCD例1：已知如图,αβ,⊥在α与β的交线上取线段AB=4cm，AC、ＢD分别在两个平面内都垂直于交线AB，并且AC=3cm，BD=12cm，求CD的长.变式练习1：如图，90PA平面ABC,ABC=，则图中互相垂直的面有（）对A.2B.3C.4D.5PABCB例2.已知RtABC中，AB＝AC＝a，D为BC的中点，以AD为折痕使BDC成直角。（1）求证：平面ABD平面BDC、平面ACD平面BDC；（2）求BAC的大小.ABCDABDC平面ACD平面ABD（1）（2）小结直线AB平面β平面α平面β。直线AB平面α3、“转化思想”.2、两个平面垂直的判定定理和性质定理.线面垂直线线垂直面面垂直1、两个平面垂直的定义.空间平面作业2、完成教材Ｐ54：A组、B组练习3、完成课后拓展学案.1、复习本节内容.变式练习2：空间四边形ABCD中，已知AC=AD，BCBD，O是CD的中点，求证：平面ABO⊥平面BCD.ACBDOACBDO思考：课本55页B组3.PCDABO平面1.如图，ABCD是正方形，SA平面ABCD，E为SE的中点，求证：（1）OE平面ABCD（2）平面BDE平面ABCD（3）ACBESABCDOE2.已知PA⊥平面ABCD，ABCD为矩形，PA=AD，M、N分别是AB、PC的中点，求证：（1）MN//平面PAD；（2）平面PMC⊥平面PDCPABCDMNE2．如图，在直四棱柱A1B1C1D1－ABCD中，当底面四边形ABCD满足条件_________时，有A1B⊥B1D1．(注：填上你认为正确的一种条件即可，不必考虑所有可能的情形.)B1C1A1D1BACDBDACABCD是菱形35.如图：PA⊥平面ABCD，ABCD是矩形,PA=AB=1，AD=，点F是PB的中点，点E在边BC上移动.（1）求三棱锥E-PAD的体积;（2）当点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；（3）证明：无论点E在边BC的何处，都有PEAF.⊥EAFPC∥平面AFPBC平面