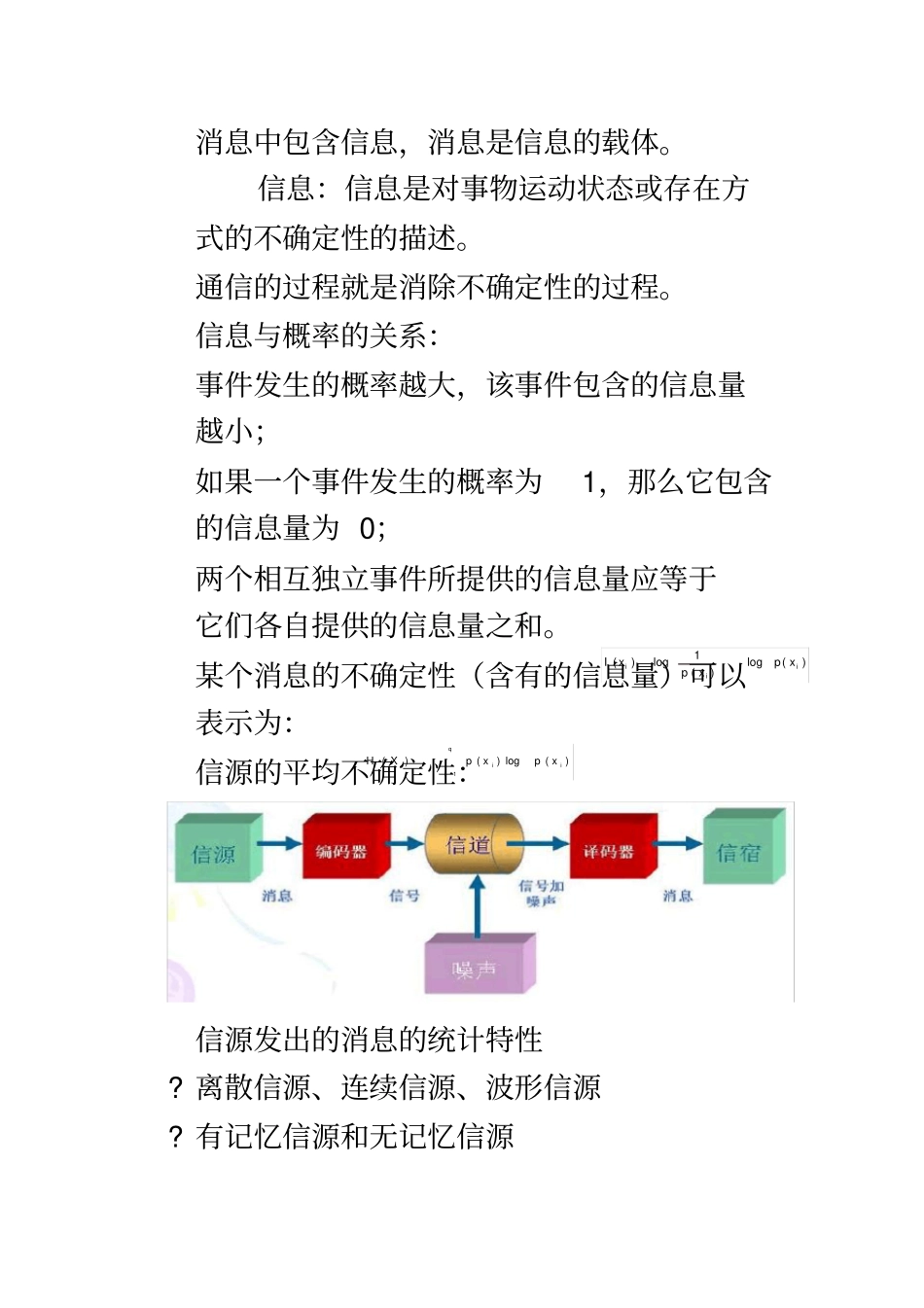
信息论期末总结消息中包含信息,消息是信息的载体。信息:信息是对事物运动状态或存在方式的不确定性的描述。通信的过程就是消除不确定性的过程。信息与概率的关系:事件发生的概率越大,该事件包含的信息量越小;如果一个事件发生的概率为1,那么它包含的信息量为0;两个相互独立事件所提供的信息量应等于它们各自提供的信息量之和。某个消息的不确定性(含有的信息量)可以表示为:信源的平均不确定性:信源发出的消息的统计特性?离散信源、连续信源、波形信源?有记忆信源和无记忆信源1()loglog()()iiiIxpxpxqiiixpxpXH1)(log)()(?平稳信源和非平稳信源编码器的功能:将消息变成适合信道传输的信号编码器包括:(1)信源编码器(2)信道编码器(3)调制器信源编码器:去除信源消息中的冗余度,提高传输的有效性信道编码器:将信源编码后的符号加上冗余符号,提高传输的可靠性。调制器:功能:将信道编码后的符号变成适合信道传输的信号目的:提高传输效率信道的统计特性无噪声信道、有噪声信道离散信道、连续信道、波形信道有记忆信道和无记忆信道恒参信道(平稳信道)和随参信道(非平稳信道)单用户信道和多用户信道信道传输信息的最高速率:信道容量译码器的功能:从接收到的信号中恢复消息。包括:(1)解调器(2)信道译码器(3)信源译码器提高有效性:(数据压缩)信源编码:无失真信源编码和限失真信源编码提高可靠性:(可靠传输)信道编码香农第一定理:如果编码后的信源序列的编码信息率不小于信源的熵,那么一定存在一种无失真信源编码方法;否则,不存在这样的一种无失真信源编码方法。香农第二定理:如果信道的信息传输率小于信道容量,那么总可以找到一种编码方式,使得当编码序列足够长时传输差错任意小;否则,不存在使差错任意小的信道编码方式。香农第三定理:对于任意的失真度,只要码字足够长,那么总可以找到一种编码方法,使编码后的编码信息率,而码的平均失真度。公理性条件:(1)如果p(x1)
I(x2),I(xi)0D()RDdD是p(xi)的单调递减函数;(2)如果p(xi)=0,则I(xi)→∞;如果p(xi)=1,则I(xi)=0;(3)由两个相对独立的事件所提供的信息量,应等于它们分别提供的信息量之和:I(xiyj)=I(xi)+I(yj)自信息可以从两个方面来理解:自信息是事件发生前,事件发生的不确定性。自信息表示事件发生后,事件所包含的信息量。先验概率:信源发出消息的概率。后验概率:信宿收到消息后推测信源发出的概率,即条件概率。互信息有两方面的含义:?表示事件出现前后关于事件的不确定性减少的量;?事件出现以后信宿获得的关于事件的信息量。观察者站在输出端ix()ipxjyix(|)ijpxy(;)()(|)log()log(|)(1,2,,;1,2,,)(|)log()ijiijiijijiIxyIxIxypxpxyinjmpxypxjyixjyixI(xi;yj)=logp(xi|yj)–logp(xi)=I(xi)–I(xi|yj)?观察者站在输入端I(yj;xi)=logp(yj|xi)–logp(yj)=I(yj)–I(yj|xi)当后验概率大于先验概率时,互信息为正。当后验概率小于先验概率时,互信息为负。当后验概率与先验概率相等时,互信息为零。任何两个事件之间的互信息不可能大于其中任一事件的自信息例6:居住某地区的女孩中有25%是大学生,在女大学生中有75%是身高1.6m以上的,而女孩中身高1.6m以上的占总数一半。假如我们得知“身高1.6m以上的某女孩是大学生”的消息,问获得多少信息量?例7:已知信源发出和两种消息,且。此消息在二进制对称信道上传输,信道传输特性为求互信息量和。自信息是一个随机变量:自信息是指信源发出的某一消息所含有的信息量。不同的消息,它们所含有的信息量也就不同。121()()2papa11221221(|)(|)1,(|)(|)pbapbapbapba)(1;1baI12;Iab平均自信息(信息熵/信源熵/香农熵/无条件熵/熵函数/熵)例2:一信源有6种输出符号,概率分别为P(A)=0.5,P(B)=0.25,P(C)=0.125,P(D)=P(E)=0.05,P(F)=0.025。1)计算H(X)。2)求符号序列ABABBA和FDDFDF的信息量,并将之与6位符号的信息量期望值相比较。递增性(递推性)例4:利用递推性计算熵函数H(1/3,1/3,1/6,1/6)的值极值性(最大离散熵定理)定理:离散无记忆信源输出n个不同的信息1()[()][log()]()log()niiiiiHXEIxEpxpxpx...