高考数学复习(数量积)课件VIP免费

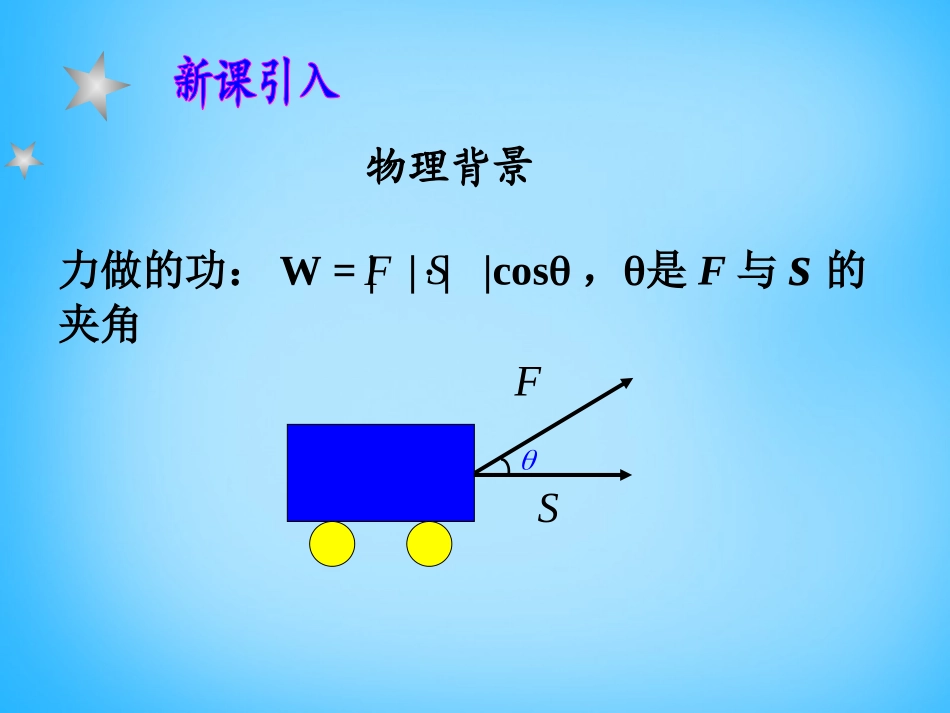
FS力做的功：W=||||cos，是F与s的夹角FS物理背景已知两个非零向量a与b，在平面上任取一点O，作OAa�，OBb�，则AOB叫做向量a与b的夹角，记作,ab．OAaBb共起点若没有，则须通过平移使它们有公共起点,,abba一.两个向量的夹角0,abOABabOABabOABab与同向ab与反向ab与垂直，ab规定：在讨论垂直问题时，零向量与任意向量垂直.记作ab,0ab,ab,2abalO1A1axlAO正射影（射影）是一个向量1、定义：已知向量和轴l，作=，过点O，A分别作轴l的垂线，垂足分别为O1，A1，则向量叫做向量在轴l上的正射影(射影).OA�11OA�aaa二.向量在轴上的正射影abOA1abOA1abOababOOA1A12、正射影的数量向量a在轴l上的正射影的坐标，称作向量a在轴l上的数量或在轴l方向上的数量．coslaala记为例1、已知轴l：（1）向量5,,60OAOAl�，求OA�在轴l上的正射影的数量1OA；155cos2OA60（2）向量5,,120OBOBl�，求OB�在轴l上的正射影的数量1OB．155cos2OB120已知两个非零向量a与b，它们的夹角为,ab，我们把cos,abab，叫做向量a与b的数量积或(内积)记作ab，即cos,ababab三.平面向量的数量积实数1、定义0a0a00影响数量积的大小的因素有哪些？两个向量的模及其夹角cos,ababab三.平面向量的数量积数量积ab等于a的长度与b在方向上正射影的数量cos,bab的乘积.θBAb�OB1cosba�2、几何意义cos,abbaba例2、已知5,4,,120,求ababab10ab×=-cos,aae1aeea（）0ab2ab（）？证明向量垂直的依据3,,,,abababab（）同向时反向时abab2,aaaaaa特别地，设a、b为两个非零向量，e是单位向量.3．两个向量的数量积的性质4abab（）abab5cos（）求夹角例3.判断正误并说明理由×××××√（1）若0a，则对任意向量b，有0ab（2）若0a，则对任意非零向量b，有0ab（3）若0a，且0ab，则0b（4）若0ab，则0a或0b（5）对任意向量a有22aa（6）若0a，且abac，则bc例4、已知3,6,ab在下列条件下，分别求ab1ab∥2ab3,60ab1,18ababab、同向时,18ababab、反向时20ab3cos609abab0<,02ab时<,02ab时例5、如图，已知正△ABC的边长为2，,,设,求BCaCAbABcabbcca�cos1202abab2bcca原式=6ABCabc33,3,0,变式：已知=,==2且求abcabcabbccaacbcos900ababcos1509bcbccos1203cabc12abbcca1、本节课主要内容有哪些？2、渗透了哪些数学思想？3、本节课有什么收获？