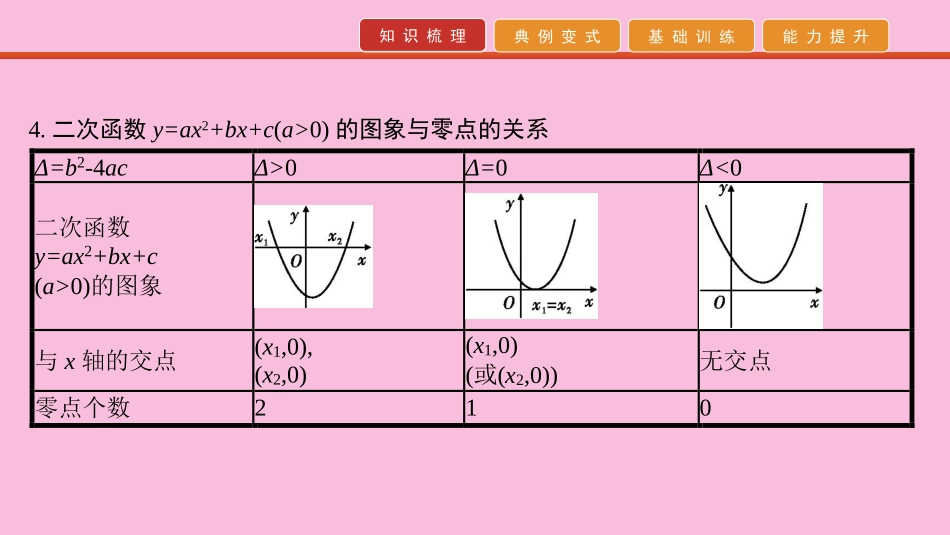
知识梳理典例变式基础训练能力提升第17讲函数与方程知识梳理典例变式基础训练能力提升知识梳理1.函数的零点(1)函数零点的定义:对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点.(2)三个等价关系:方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有零点.2.函数零点的判定如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是f(x)=0的根.我们把这一结论称为函数零点存在性定理.3.明确三个等价关系(三者相互转化)知识梳理典例变式基础训练能力提升知识梳理4.二次函数y=ax2+bx+c(a>0)的图象与零点的关系Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象与x轴的交点(x1,0),(x2,0)(x1,0)(或(x2,0))无交点零点个数210知识梳理典例变式基础训练能力提升典例变式题型一函数零点所在区间的判断【例1】(1)函数f(x)=lnx-的零点所在的大致区间是()A.(1,2)B.(2,3)C.(1,e)和(3,4)D.(e,+∞)(2)设f(x)=0.8x-1,g(x)=lnx,则函数h(x)=f(x)-g(x)存在的零点一定位于下列哪个区间()A.(0,1)B.(1,2)C.(2,e)D.(e,3)2x知识梳理典例变式基础训练能力提升典例变式【解析】(1)因为f'(x)=1x+2x2>0(x>0),所以f(x)在(0,+∞)上单调递增,又f(3)=ln3-23>0,f(2)=ln2-1<0,所以f(2)·f(3)<0,所以f(x)唯一的零点在区间(2,3)内.故选B.(2)h(x)=f(x)-g(x)的零点等价于方程f(x)-g(x)=0的根,即为函数y=f(x)与y=g(x)图象的交点的横坐标,其大致图象如图,从图象可知它们仅有一个交点A,横坐标的范围为(0,1),故选A.【答案】(1)B(2)A知识梳理典例变式基础训练能力提升典例变式【规律总结】判断函数零点所在区间的三种方法(1)解方程法:当对应方程f(x)=0易解时,可先解方程,然后再看求得的根是否落在给定区间上.(2)定理法:利用函数零点的存在性定理,首先看函数y=f(x)在区间[a,b]上的图象是否连续,再看是否有f(a)·f(b)<0.若有,则函数y=f(x)在区间(a,b)内必有零点.(3)图象法:通过画函数图象,观察图象与x轴在给定区间上是否有交点来判断.知识梳理典例变式基础训练能力提升典例变式变式训练一已知函数f(x)=lnx-12x-2的零点为x0,则x0所在的区间是()A.(0,1)B.(1,2)C.(2,3)D.(3,4)C【解析】因为f(x)=lnx-12x-2在(0,+∞)上是增函数,又f(1)=ln1-12-1=ln1-2<0,f(2)=ln2-120<0,f(3)=ln3-121>0,所以x0∈(2,3),故选C.知识梳理典例变式基础训练能力提升典例变式题型二函数零点个数的问题【例2】(1)函数f(x)=ቊx2+x-2,x≤0,-1+lnx,x>0的零点个数为()A.3B.2C.1D.0(2)(2019·泰安模拟)已知函数f(x)=൜log2x,x>0,3x,x≤0,若关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是.知识梳理典例变式基础训练能力提升典例变式【解析】(1)法一:由f(x)=0得൜x≤0,x2+x-2=0或൜x>0,-1+lnx=0,解得x=-2或x=e.因此函数f(x)共有2个零点.法二:函数f(x)的图象如图所示,由图象知函数f(x)共有2个零点.知识梳理典例变式基础训练能力提升典例变式(2)问题等价于函数y=f(x)与y=-x+a的图象有且只有一个交点,作出函数f(x)的图象(如图所示),结合函数图象可知a>1.【答案】(1)B(2)(1,+∞)知识梳理典例变式基础训练能力提升典例变式【规律方法】判断函数零点个数的三种方法(1)方程法:令f(x)=0,如果能求出解,则有几个解就有几个零点.(2)零点存在性定理法:利用定理不仅要求函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点或零点值所具有的性质.(3)数形结合法:转化为两个函数的图象的交点个数问题.先画出两个函数的图象,看其交点的个数,其中交点的横坐标有几个不同的值,就有几个不同的零点.知识梳理典例变式基础训练能力提升典例变式变式训练二1.函数f(x)=|x-2|-lnx在定义域内的零点的个数为()A.0B.1C.2D.3C【解析】由题意可知f(x)的定义域为(0,+∞),在同一直角坐标系中画出函数y1=|x-2|(x>0),y2=lnx(x>0)的图象,如图所示.由图可知函数f(x)在定义域内的零点个数为2.知识梳理典例变式基础训练能力提升典例变式2.已知函数f(x)=൜x+1,x≤0,log2x,x>0,则函数y=f(f(...