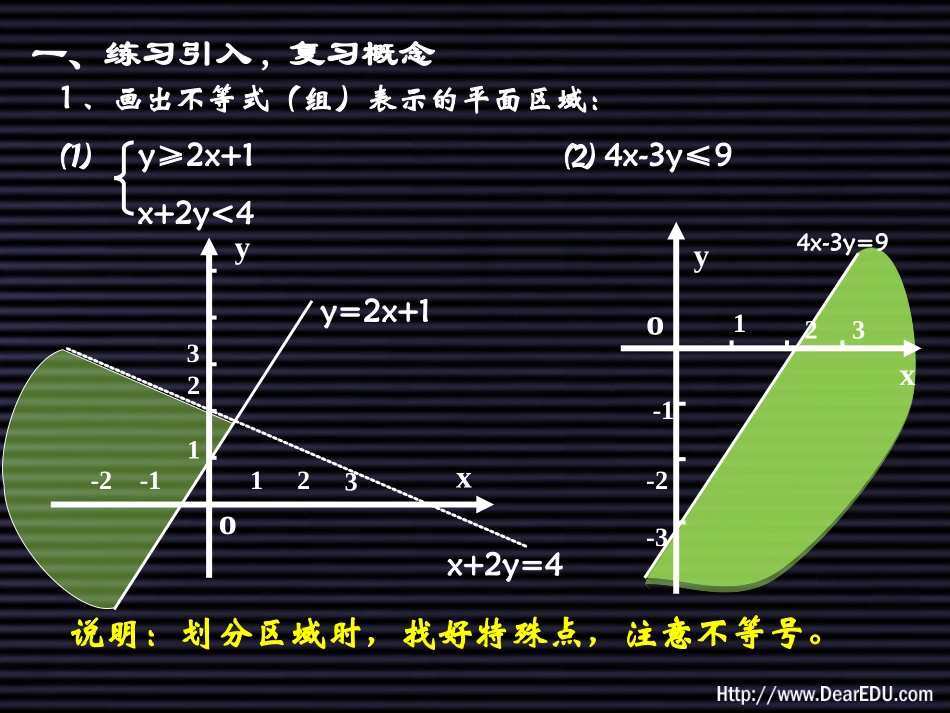
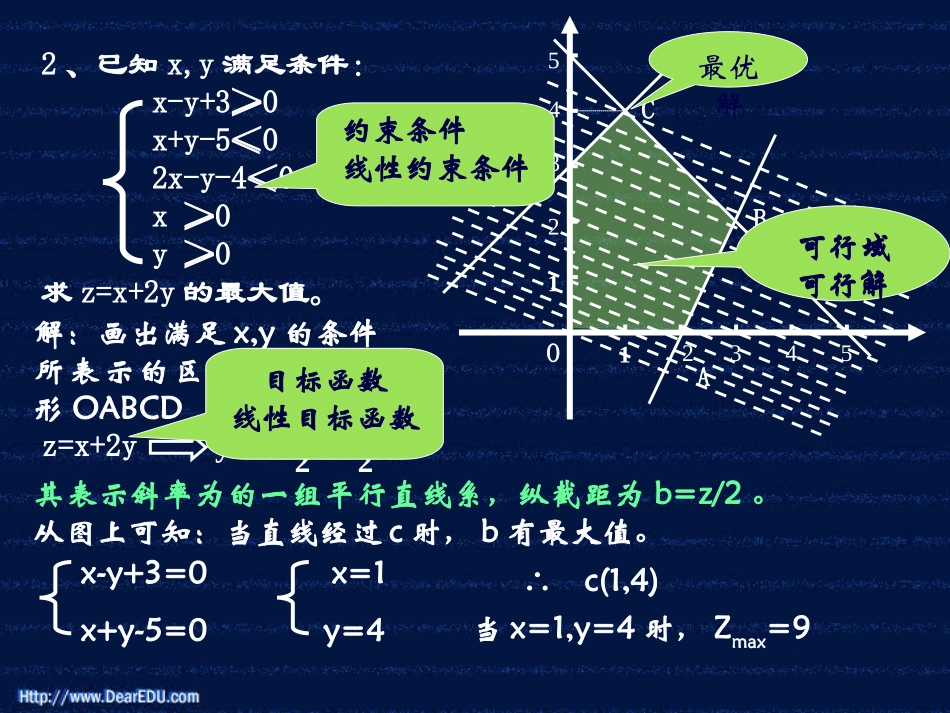
简单的线性规划1、画出不等式(组)表示的平面区域:⑴y≥2x+1⑵4x-3y≤9x+2y<4说明:划分区域时,找好特殊点,注意不等号。xo123-1-2-3y4x-3y=9一、练习引入,复习概念yoxy=2x+1x+2y=4112233-1-22、已知x,y满足条件:x-y+3≥0x+y-5≤02x-y-4≤0x≥0y≥0求z=x+2y的最大值。解:画出满足x,y的条件所表示的区域,即五边形OABCD(如图)z=x+2yy=+xz22DA1234512345OBC其表示斜率为的一组平行直线系,纵截距为b=z/2。从图上可知:当直线经过c时,b有最大值。x-y+3=0x=1x+y-5=0y=4∴c(1,4)当x=1,y=4时,Zmax=9约束条件线性约束条件目标函数线性目标函数最优解可行域可行解1、咖啡屋配制两种饮料,成分配比和单价如下表:饮料奶粉(杯)咖啡(杯)糖(杯)价格(杯)甲种9(g)4(g)3(g)0.7(元)乙种4(g)5(g)10(g)1.2(元)每天使用限额为奶粉3600g,咖啡2000g,糖3000g,若每天在原料的使用限额内饮料能全部售出,应配制两种饮料各多少杯获利最大?二、例题选讲解:设每天配制甲种饮料x杯,乙种y杯,则线性约束条件为:9x+4y≤36004x+5y≤20003x+10y≤3000画出可行域(阴影部分),即五边形ABCDO9x+4y=36003x+10y=30004x+5y=2000OABCD200200目标函数z=0.7x+1.2yy=-x+z从图可知:当直线l过B点时,y轴截距最大,即z最大。9x+4y=3600x=∴B(,)4x+5y=2000y=∴当x=,y=时,Zmax=0.7x+1.2y=390.3元1000291000293600293600297121012100029360029l9x+4y=36003x+10y=30004x+5y=2000OABCD200200正确答案:1)线性约束条件为:9x+4y≤36004x+5y≤20003x+10y≤3000x∈Ny∈N当l过点C时,y轴截距b最大,即z最大∴当x=200,y=240时,Zmax=0.7×200+1.2×240=428(元)答:每天应配制甲种饮料200杯,乙种饮料240杯时,获利最大。3x+10y=3000y=240解4x+5y=2000得x=200∴C(200,240)y=240l说明:约束条件要写全,求解过程要细心,解题格式要规范。z=0.7x+1.2yy=-x+z7121012目标函数:yx2、已知函数f(x)=ax2-c,满足-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围。-4≤f(1)≤-1-4≤a-c≤-10≤a≤3-1≤f(2)≤5-1≤4a-c≤51≤c≤7解:依题意:而所求f(3)=9a-c0≤9a≤27-7≤-c≤-1∴-1≤f(3)≤26∴-7≤9a-c≤26正解一:依题意得:f(1)=a-cf(2)=4a-c可知:f(3)=9a-c=-5/3f(1)+8/3f(2) -4≤f(1)≤-1,-1≤f(2)≤5∴5/3≤-5/3f(1)≤20/3,-8/3≤8/3f(2)≤40/3∴-1≤-5/3f(1)+8/3f(2)≤20即:-1≤f(3)≤20正解二:线性约束条件:目标函数:t=f(3)=9a-c-4≤a-c≤-1-1≤4a-c≤5作出约束条件的可行域:为平行四边形ABCD,平行直线系t=9a-c,c=9a-t,斜率为9。ac224646-2-28-4-4o说明:约束条件变化时要用等价变换DABC(3,7)当平行直线过A(0,1)时,tmin=9×0-1=-1过点C(3,7)时,tmax=9×3-7=20∴-1≤f(3)≤20四、课堂小结1、通过例题更清楚地理解了线性规划相关概念。2、正确作图,充分应用数形结合思想解题。3、求解目标函数时,一定要找到几何支撑点。4、作业要严谨细致,严格规范。五、作业:课课练:P672,6,P692,3有一批同规划钢条,有两种切割方式,可截成长度为a的2根,长度为b的3根,或截成长度为a的3根,长度为b的1根。⑴现需2根a长与1根b长配成一套,问按两种切割方式进行切割应满足的比例是多少?⑵如果长度为a的至少需50根,长度为b的至少需45根,问如何切割可使钢条用量最省?2X+3Y3x+y=12由:P=YX求得41=目标函数:P=YX解:设第一种切割方式需x根,第二种切割方式需y根则1)约束条件组:Y∈N2X+3Y3x+y=12x∈N规格第一种x根第二种y根总计要求a2x3y2x+3y2:1b3xy3x+y分析:练习3x+y=4515302x+3y=50yx15453045A由2x+3y=503x+y=45X=85/7Y=60/7∴A(85/7,60/7),tmin=x+y=145/7⑵分析:a长度的总数要不少于50根,b长度的总数不少于45根,其目标函数为t=x+y,求其最小值。可行域为如图阴影部分解:线性约束条件组:x≥0y≥02x+3y≥503x+y≥45O线性目标函数:t=x+y,y=-x+t由图:当直线系y=-x+t移到A点时,纵截距最大,即t最小。所求钢条数是整数,故所求x,y为整数。即找可行域内的整数点。用平行找解法,l向右上方平移,在可行域中最先经过整数点(12,9),(13,8),此时t=21,即为最小值。由tmin=145/7,当t=21(为什么不取不足...