高中数学 定积分的简单应用课件2 新人教A版选修2-2 课件VIP免费

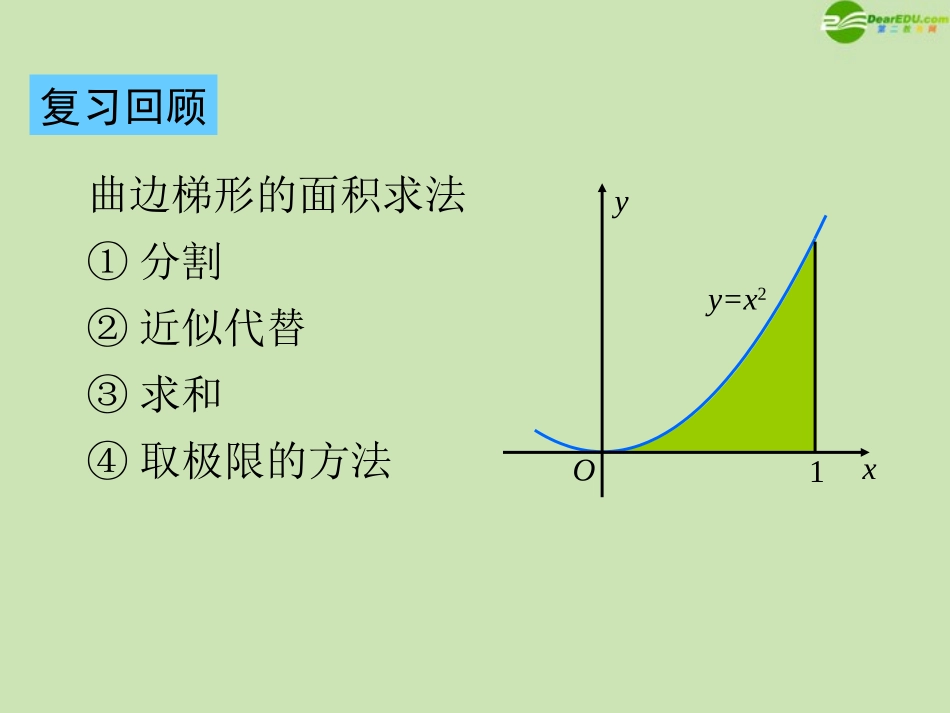
汽车行驶的路程曲边梯形的面积求法①分割②近似代替③求和④取极限的方法复习回顾y=x2xyO1思考汽车以速度v作匀速直线运动时,经过时间t所行驶的路程为S=vt.如果汽车作变速直线运动,在时刻t的速度为v(t)=-t2+2(单位:km/h),那么它在0≤x≤1(单位:h)这段时间内行驶的路程S(单位:km)是多少?y=x2xyO1以直代曲以不变代变在小区间内可以认为汽车近似于作匀速直线运动(1)分割在[0,1]间插入n-1个分点：分成n个小区间：1,1,2,1,1,0nnnnnniiSS1记第i个区间为nninitninini11,,2,1,1其长度为对应的路程为△Si(2)近似代替ninnninnitnivSSii,,2,12111211'22△t→0上在区间nini,1nivtv1局部小围范内“以匀速代变速”(3)求和niniintnivSS111'ninnni12211211111022nnnnnn212112223nn2612113nnnn22111131nn22111131nnSSn(4)取极限3522111131lim11limlim1nnnivnSSnninnn△t0SnSn∞探究结合求曲边梯形面积的过程,你认为汽车行驶的路程S与由直线t=0,t=1,v=0和曲线v=-t2+2所围成的曲边梯形的面积有什么关系?△SiniinSS1'nnSSlim汽车路程与曲边梯形的面积数值上相等21Otvv=－t2+2堂上练习?35,?S,S,2,,,2,1,1,"".12吗这个值是出若能求的值吗用这种方法能求出的近似值路程从而得到汽车行驶的总作匀速行驶处的速度汽车近似地以时刻上时间间隔如果我们认为在每个小中近似代替在上面的第二步ninivnininini堂上练习2.一辆汽车在笔直的公路上变速行驶,设汽车在时刻t的速度为v(t)=－t2＋5(单位:km/h),度计算这辆汽车在0≤t≤2(单位:h)这段时间内汽车行驶的路程S(单位:km).