高二数学定积分课件 苏教版 课件VIP免费

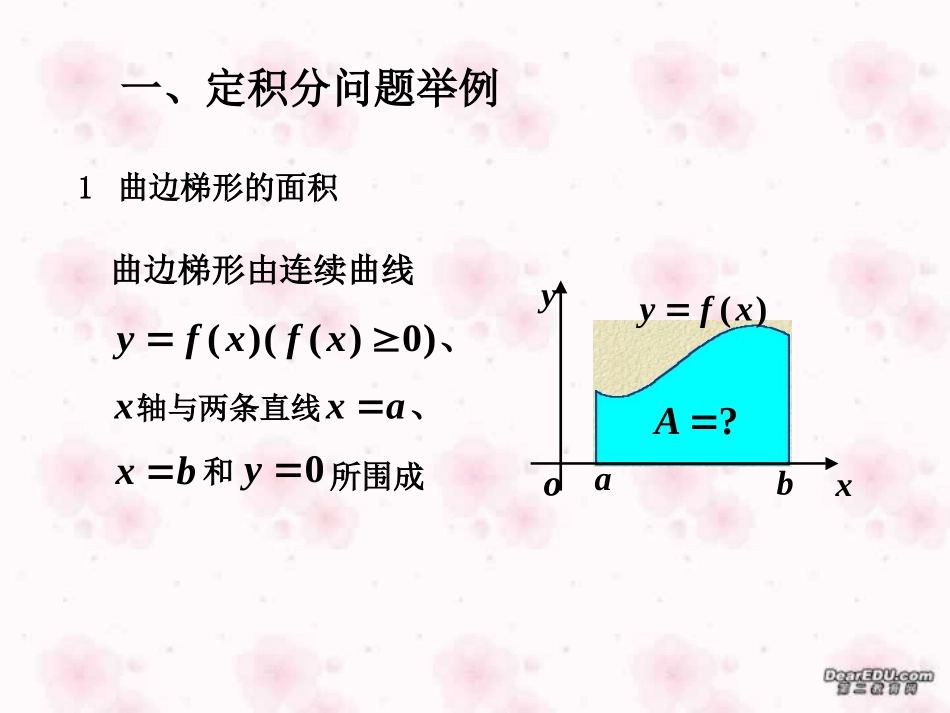
定积分江苏省扬中高级中学卞国文8.1定积分三、定积分的性质一、定积分问题举例二、定积分的定义abxyo?A曲边梯形由连续曲线1曲边梯形的面积)(xfy)0)((xf、x轴与两条直线ax、一、定积分问题举例)(xfybx0y所围成和abxyoabxyo用矩形面积近似取代曲边梯形面积显然，小矩形越多，矩形总面积越接近曲边梯形面积．（四个小矩形）（九个小矩形）曲边梯形如图,1210],[bnxnxxxxaba内插入若干个分点，在区间abxyoiix1x1ix1nx;],[],[11iiiiixxxxxnba长度为，个小区间分成把区间，上任取一点在每个小区间iiixx],[1iiixfA)(为高的小矩形面积为为底，以)(],[1iiifxxiniixfA)(1曲边梯形面积的近似值为时，趋近于零即小区间小区间的最当分割无限加细0)(λ}Δx,Δx,xmax{λ,n21iniixfA)(lim10曲边梯形面积为2变速直线运动的路程设某物体作直线运动，已知速度)(tvv是时间间隔],[21TT上t的一个连续函数，且0)(tv，求物体在这段时间内所经过的路程.思路：把整段时间分割成若干小段，每小段上速度看作不变，求出各小段的路程再相加，便得到路程的近似值，最后通过对时间的无限细分过程求得路程的精确值．（1）分割212101TtttttTnn1iiitttiiitvs)(部分路程值某时刻的速度（2）求和iinitvs)(1（3）取极限},,,max{21ntttiniitvs)(lim10路程的精确值记},,,max{21nxxx，如果不论对],[ba二、定积分的定义设函数)(xf在],[ba上有界，在],[ba中任意插入若干个分点bxxxxxann1210把区间],[ba分成n个小区间，各小区间的长度依次为1iiixxx，),2,1(i，在各小区间上任取一点i（iix），作乘积iixf)(),2,1(i并作和iinixfS)(1，定义怎样的分法，也不论在小区间],[1iixx上点i怎样的取法，只要当0时，和S总趋于确定的极限I，我们称这个极限I为函数)(xf在区间],[ba上的定积分，记为baIdxxf)(iinixf)(lim10被积函数被积表达式积分变量积分区间],[ba积分上限积分下限积分和注：（1）积分值仅与被积函数及积分区间有关，badxxf)(badttf)(baduuf)(（2）定义中区间的分法和i的取法是任意的.而与积分变量的字母无关.（3）当函数)(xf在区间],[ba上的定积分存在时，称)(xf在区间],[ba上可积.当函数)(xf在区间],[ba上连续时，定理1称)(xf在区间],[ba上可积.存在定理定理2设函数)(xf在区间],[ba上有界，且只有有限个间断点，则)(xf在区间],[ba上可积.,0)(xfbaAdxxf)(曲边梯形的面积,0)(xfbaAdxxf)(曲边梯形的面积的负值1A2A3A4A4321)(AAAAdxxfba定积分的几何意义几何意义：积取负号．轴下方的面在轴上方的面积取正号；在数和．之间的各部分面积的代直线的图形及两条轴、函数它是介于xxbxaxxfx,)(例1利用定义计算定积分.102dxx解将]1,0[n等分，分点为nixi，(ni,,2,1)小区间],[1iixx的长度nxi1，(ni,,2,1)取iix，(ni,,2,1)iinixf)(1iinix21,12iniixxnnini121niin12316)12)(1(13nnnn,121161nnn0dxx102iinix210limnnn121161lim.31例2利用定义计算定积分.121dxx解在]2,1[中插入分点12,,,nqqq,典型小区间为],[1iiqq，（ni,,2,1）小区间的长度)1(11qqqqxiiii,取1iiq，（ni,,2,1）iinixf)(1iniix11)1(1111qqqiniiniq1)1()1(qn取2nq即nq12)12(lim1xxxxxx112lim1,2ln)12(lim1nnn,2lndxx211iniix101lim)12(lim1nnn.2ln),12(1nniinixf)(1例3设函数)(xf在区间]1,0[上连续，且取正值.nnnnfnfnf21lim...