高中数学椭圆的参数方程1新人教A版选修4-4 课件VIP免费

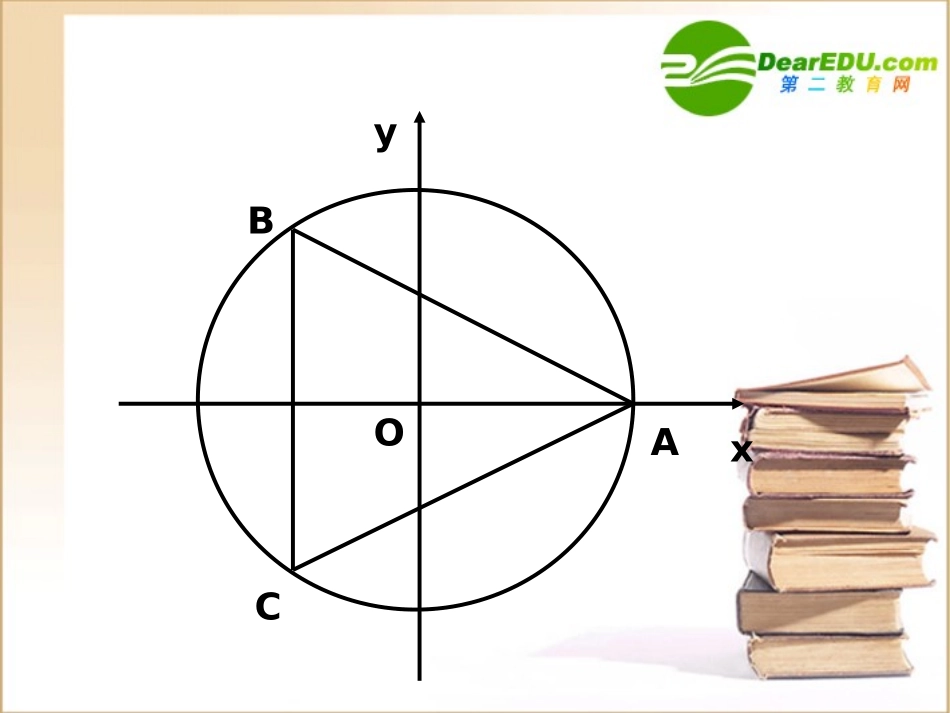
)(21100{12为参数，表示时间、tgthytx)(4132{,41,32),,(2为参数以时间的轨迹的参数方程为于是点则，动点的位置是、设经过时间ttytxMtytxyxMtxyACBO6])23(sin)21[(cos])23(sin)21[(cos]sin)1[(cos)sin,(cos)23,21(),23,21(),0,1(,,)(sincos{,13222222222MCMBMAMCBAyxxCBABC则设点的坐标分别为为参数是那么外接圆的参数方程轴对称关于，时点如图的平面直角坐标系，建立的外接圆的半径为、解：不妨设双曲线；）（一段抛物线；为端点的以）（直线；、解,43)2,1(),2,1(],1,1[,22,072)1(;4222yxxxyyx)(sincos){2()(113){1(5442为参数为参数、ayaxttyttx二、圆锥曲线的参数方程1、椭圆的参数方程参数方程。轴上的椭圆的，焦点在这是中心在原点为参数一个参数方程为的我们得到了椭圆由例xObyaxbabyax)(sincos{)0(142222的意义是什么？方程中参数数的意义，椭圆的参数类比圆的参数方程中参思考：xyoAMBsinsincoscos,,),(bOByaOAxBAyBxAyxMOAox定义有的的终边上，由三角函数均在角，由点的纵坐标为点的横坐标为，那么点是的坐标，点为终边的角为始边，设以轴上的椭圆。，焦点在这是中心在原点为参数是的轨迹，它的参数方程点旋转一周时，就得到了绕点当半径xObyaxMOOA)(sincos{)2,0[范围是的通常规定参数在椭圆的参数方程中，的意义类似吗？中参数为参数程的意义与圆的参数方椭圆的参数方程中参数思考：)(sincos{ryrx的旋转角。是半径的旋转角，参数是，不的离心角称为点的旋转角或径所对应的圆的半是点由图可以看出，参数OMOMMOBOAM)()(sincos{)(sincos{.1111{222222byaxyxyxbyaxybyxax方程为可以得到椭圆的参数为参数利用圆的参数方程＋可以变成则椭圆的方程通过伸缩变换从几何变换的角度看，椭圆参数方程的推导xoyAMB)2,0(),3,1()0,3(),3,2()sin2,cos3(1、点、点、点、点确定的曲线必过所变化时，动点、当参数DCBAP它的焦距是多少？()B52?____________________)(,0cos3sin2cos42222方程为通，那么圆心的轨迹的普为参数、已知圆的方程为yxyx14)(sincos2{1)sin()cos2(0cos3sin2cos42222222yxyxyxyxyx化为普通方程是为参数所以圆心的参数方程为可以化为解：方程.______________,__________)(2sin8cos173{3准线方程为为的中心坐标为参数、椭圆yx)2,3(152893x小节：椭圆的参数方程的形式椭圆参数方程中参数的意义