高中数学 第三章(不等式)含参数的不等式恒成立问题的解法课件 北师大版必修5 课件VIP免费

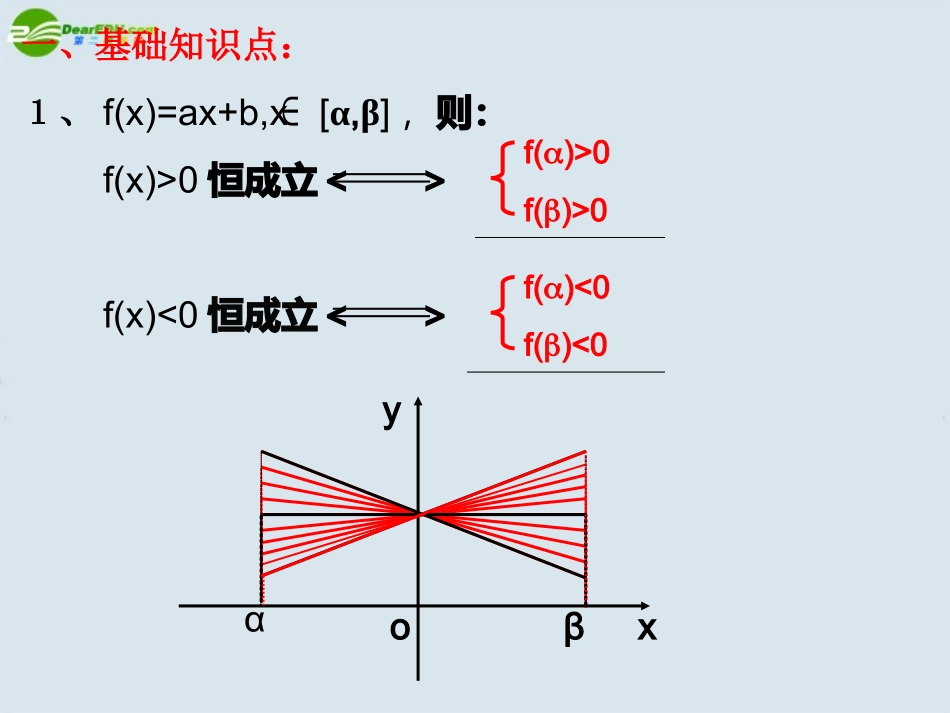
北师大版高中数学必修5第三章《不等式》一、基础知识点：１、f(x)=ax+b,x[α,β]，则：f(x)>0恒成立＜＞f(x)<0恒成立＜＞αβoxyf()>0f()>0f()<0f()<0２、ax2+bx+c>0在R上恒成立的充要条件是：______________________。a=b=0C>0或a>0Δ=b2-4ac<0ax2+bx+c<0在R上恒成立的充要条件是：______________________。a=b=0C<0或a<0Δ=b2-4ac<0３、ａ≥f(x)恒成立的充要条件是：_____________;ａ≤f(x)恒成立的充要条件是：_____________。ａ≥[f(x)]maxａ≤[f(x)]min二、典型例题：例1、对于不等式(1-m)x2+(m-1)x+3>0................(*)（1）当|x|≤2，(*)式恒成立，求实数m的取值范围；（2）当|m|≤2，(*)式恒成立，求实数x的取值范围.当1-m<0时，即m>1,(*)式在x[-2,2]时恒成立的充要条件为：解：(1)当1-m=0即m=1时，(*)式恒成立，故m=1适合(*)；(1-m)•(-2)2+(m-1)•(-2)+3>0当1-m>0时，即m<1,(*)式在x[-2,2]时恒成立的充要条件为：△=(m-1)2-12(I-m)<0，解得:-110恒成立g(-2)=3x2-3x+3>0g(2)=-x2+x+3>0解(2):设g(m)=(-x2+x)m+(x2-x+3)（m[-2,2]）即xR213121310................(*)（1）当|x|≤2，(*)式恒成立，求实数m的取值范围；（2）当|m|≤2，(*)式恒成立，求实数x的取值范围.练习1:对于一切|p|≤2，pR∈，不等式x2+px+1>2x+p恒成立，则实数x的取值范围是：——————————。x<-1或x>3小结：1、一次函数型问题，利用一次函数的图像特征求解。2、二次函数型问题，结合抛物线图像，转化成最值问题，分类讨论。例2、①若不等式x20,对x[-3,3]恒成立，则实数k的取值范围是——————————。2110xy21y=x2y=logx16141在同一坐标系下作它们的图象如右图:①解：设y1=x2(x(0,))y2=logax21由图易得:≤a＜1161≤a＜1161y=x2+22-2３-３211y=kxy=2x2y=-2x2②解：原不等式可化为：x2+2>kx例2、①若不等式x20,对x[-3,3]恒成立，则实数k的取值范围是——————————。21设y1=x2+2(x[-3,3])y2=kx在同一坐标系下作它们的图象如右图:由图易得:-20）txy解:分离参数得:a≥yxxy2x又令1+2t=m（m>1），则f(m)=2)21m(1m2)m5m(4∴a≥[f(x)]max=即a≥215215(当且仅当m=时等号成立)521525245m22mm4xy1xy21恒成立2t1t21,则a≥（t>0）恒成立小结：4、通过分离参数，将问题转化为ａ≥f(x)（或ａ≤f(x)）恒成立，再运用不等式知识或求函数最值的方法，使问题获解。例４、已知a>0，函数f(x)=ax-bx2，（1）当b>1，证明对任意的x[0,1]∈，|f(x)|≤1充要条件是:b-1≤a≤2；（2）当01∴bx+≥2(x=时取等号)bb1x1bx-≤a≤+bxx1x1解:(1)b>1时,对x(0,1],|f(x)|≤1-1≤∈ax-bx2≤1bx2-1≤ax≤1+bx2故x(0,1]∈时原式恒成立的充要条件为:b-1≤a≤2b∴(bx-)max=b-1(x=1时取得)x1又bx-在(0,1]上递增x1又x=0时，|f(x)|≤1恒成立∴x[0,1]∈时原式恒成立的充要条件为:b-1≤a≤2b故(bx+)min=b+1(x=1时取得)x1(2)00三、课时小结：2、二次函数型问题，结合抛物线图像，转化成最值问题，分...