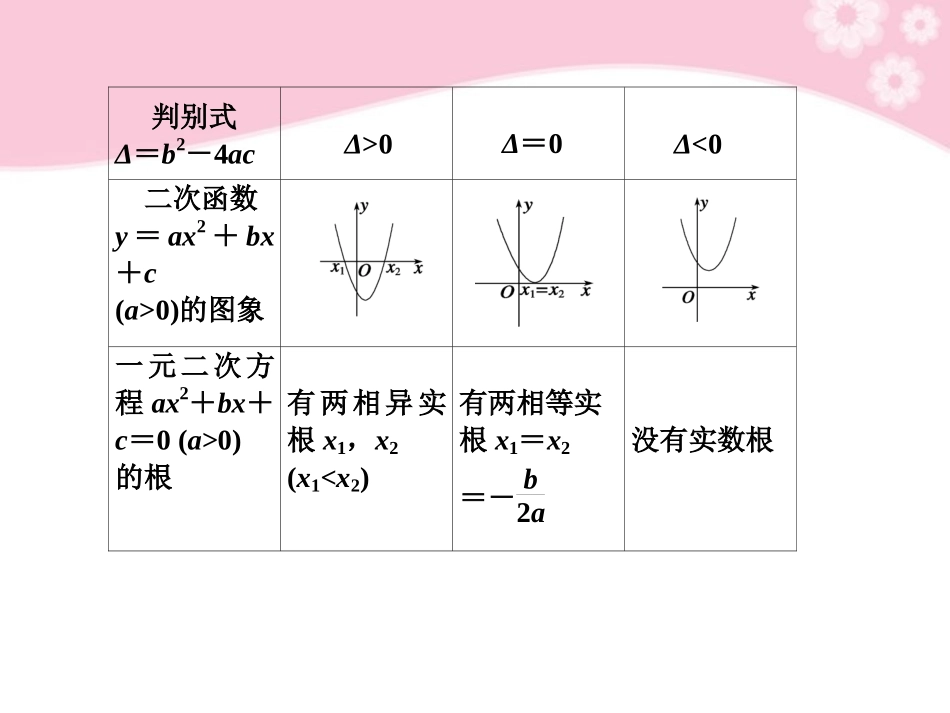
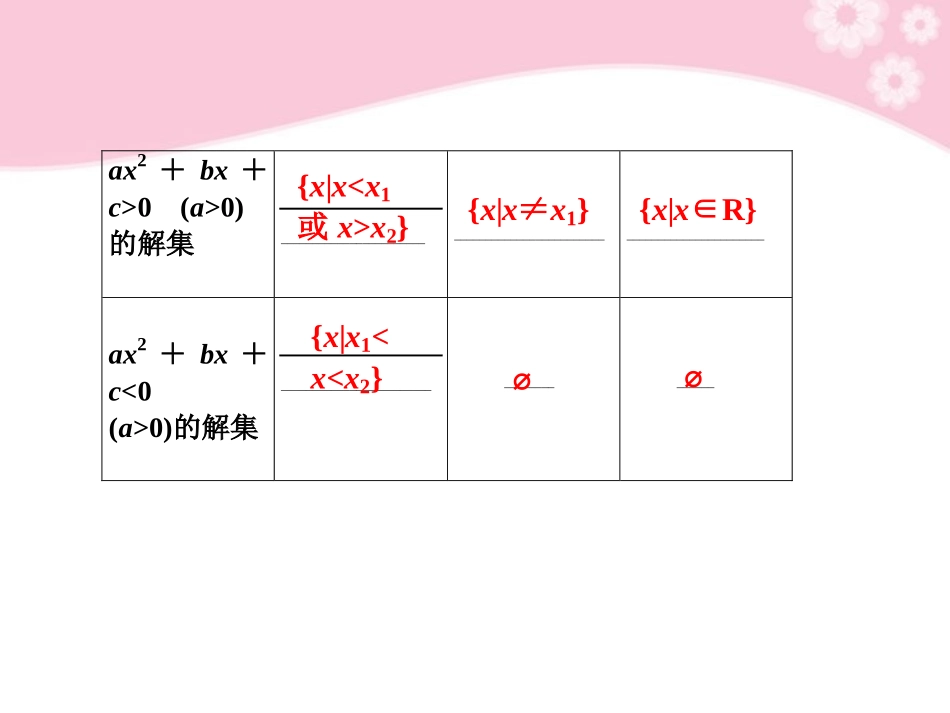
§7.2一元二次不等式及其解法基础知识自主学习要点梳理1.一元二次不等式与相应的二次函数及一元二次方程的关系如表:判别式Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象一元二次方程ax2+bx+c=0(a>0)的根有两相异实根x1,x2(x10(a>0)的解集_____________________________________________________________________ax2+bx+c<0(a>0)的解集______________________________________{x|xx2}{x|x≠x1}{x|x∈R}{x|x10(a>0)的求解的算法过程为3.上述不等式ax2+bx+c>0(<0)中的a均大于0,若a<0,则可先进行转化,使x2的系数为正,但一定注意在转化过程中,不等号的变化.[难点正本难点清源]一元二次不等式的解集及解集的确定一元二次不等式ax2+bx+c<0(a≠0)的解集的确定受a的符号、b2-4ac的符号的影响,且与相应的二次函数、一元二次方程有密切联系,可结合相应的函数y=ax2+bx+c(a≠0)的图象,数形结合求得不等式的解集.若一元二次不等式经过不等式的同解变形后,化为ax2+bx+c>0(或<0)(其中a>0)的形式,其对应的方程ax2+bx+c=0有两个不等实根x1,x2,(x10),则可根据“大于取两边,小于夹中间”求解集.基础自测1.不等式x2<1的解集为____________.解析x2<1,则-10的解集为x|-11,则x0的取值范围为()A.(-∞,-1)∪(1,+∞)B.(-∞,-1)∪[1,+∞)C.(-∞,-3)∪(1,+∞)D.(-∞,-3)∪[1,+∞)解析 f(x0)>1,∴x0≥12x0+1>1或x0<1x20-2x0-2>1,解得x0∈(-∞,-1)∪[1,+∞).B题型分类深度剖析题型一一元二次不等式的解法例1解下列不等式:(1)2x2+4x+3<0;(2)-3x2-2x+8≤0;(3)8x-1≥16x2.思维启迪:首先将二次项系数转化为正数,再看二次三项式能否因式分解,若能,则可得方程的两根,大于号取两边,小于号取中间,若不能,则再看“Δ”,利用求根公式求解方程的根,而后写出解集.解(1) Δ=42-4×2×3=16-24=-8<0.∴方程2x2+4x+3=0没有实根.∴2x2+4x+3<0的解集为∅.(2)原不等式等价于3x2+2x-8≥0⇔(x+2)(3x-4)≥0⇒x≤-2或x≥43.∴不等式的解集为(-∞,-2]∪[43,+∞).(3)原不等式等价于16x2-8x+1≤0⇔(4x-1)2≤0.∴只有当4x-1=0,即x=14时不等式成立,故不等式解集为14.探究提高解一元二次不等式的一般步骤是:(1)化为标准形式;(2)确定判别式Δ的符号;(3)若Δ≥0,则求出该不等式对应的二次方程的根,若Δ<0,则对应的二次方程无根;(4)结合二次函数的图象得出不等式的解集.特别地,若一元二次不等式的左边的二次三项式能分解因式,则可立即写出不等式的解集.变式训练1已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.(1)若A∩B=[0,3],求实数m的值;(2)若A⊆∁RB,求实数m的取值范围.解由已知得:A={x|-1≤x≤3},B={x|m-2≤x≤m+2}.(1) A∩B=[0,3],∴m-2=0,m+2≥3,∴m=2,m≥1.∴m=2.(2)∁RB={x|xm+2}. A⊆∁RB,∴m-2>3,或m+2<-1,∴m>5或m<-3.题型二含参数的一元二次不等式的解法例2求不等式12x2-ax>a2(a∈R)的解集.思维启迪:先求方程12x2-ax=a2的根,讨论根的大小,确定不等式的解集.解 12x2-ax>a2,∴12x2-ax...