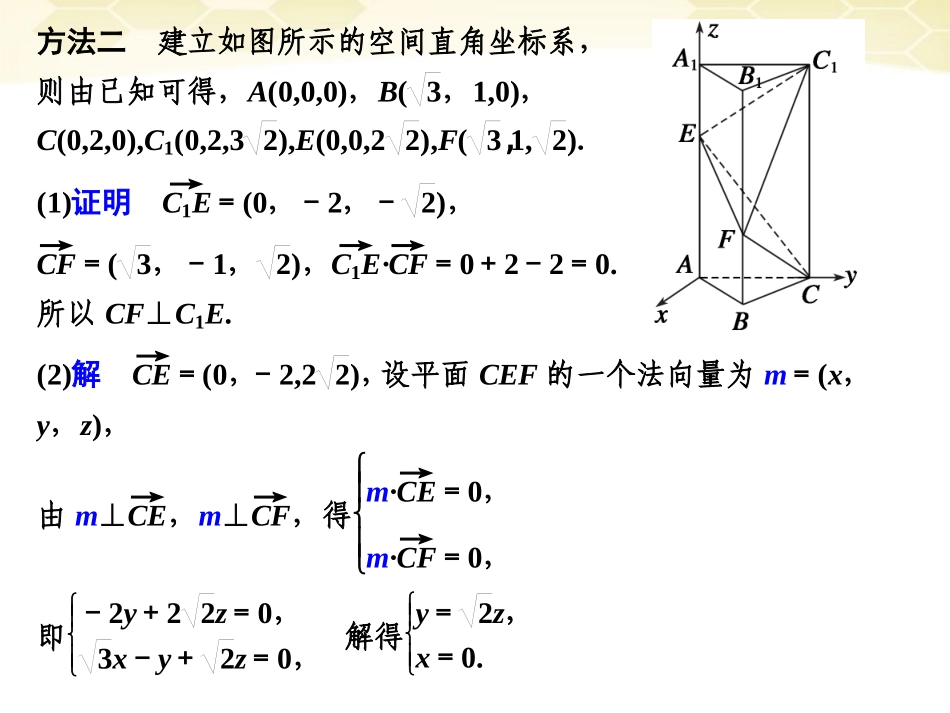
§3空间向量与立体几何真题热身(2011·湖北)如图,已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为32,点E在侧棱AA1上,点F在侧棱BB1上,且AE=22,BF=2.(1)求证:CF⊥C1E;(2)求二面角E-CF-C1的大小.方法一(1)证明由已知可得CC1=32,CE=C1F=22+(22)2=23,EF2=AB2+(AE-BF)2,EF=C1E=22+(2)2=6,于是有EF2+C1E2=C1F2,CE2+C1E2=CC21,所以C1E⊥EF,C1E⊥CE.又EF∩CE=E,所以C1E⊥平面CEF.又CF⊂平面CEF,故CF⊥C1E.(2)解在△CEF中,由(1)可得EF=CF=6,CE=23,于是有EF2+CF2=CE2,所以CF⊥EF.又由(1)知CF⊥C1E,且EF∩C1E=E,所以CF⊥平面C1EF.又C1F⊂平面C1EF,故CF⊥C1F.于是∠EFC1即为二面角E-CF-C1的平面角.由(1)知△C1EF是等腰直角三角形,所以∠EFC1=45°,即所求二面角E-CF-C1的大小为45°.方法二建立如图所示的空间直角坐标系,则由已知可得,A(0,0,0),B(3,1,0),C(0,2,0),C1(0,2,32),E(0,0,22),F(3,1,2).(1)证明C1E→=(0,-2,-2),CF→=(3,-1,2),C1E→·CF→=0+2-2=0.所以CF⊥C1E.(2)解CE→=(0,-2,22),设平面CEF的一个法向量为m=(x,y,z),由m⊥CE→,m⊥CF→,得m·CE→=0,m·CF→=0,即-2y+22z=0,3x-y+2z=0,解得y=2z,x=0.可取m=(0,2,1).设侧面BC1的一个法向量为n,由n⊥CB→,n⊥CC1→,及CB→=(3,-1,0),CC1→=(0,0,32),可取n=(1,3,0).设二面角E-CF-C1的大小为θ,于是由θ为锐角可得cosθ=|m·n||m||n|=63×2=22,所以θ=45°.即所求二面角E-CF-C1的大小为45°.考点整合1.直线与平面、平面与平面的平行与垂直的向量方法设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2).平面α、β的法向量分别为μ=(a3,b3,c3),v=(a4,b4,c4)(以下相同).(1)线面平行l∥α⇔a⊥μ⇔a·μ=0⇔a1a3+b1b3+c1c3=0.(2)线面垂直l⊥α⇔a∥μ⇔a=kμ⇔a1=ka3,b1=kb3,c1=kc3.(3)面面平行α∥β⇔μ∥v⇔μ=kv⇔a3=λa4,b3=λb4,c3=λc4.(4)面面垂直α⊥β⇔μ⊥v⇔μ·v=0⇔a3a4+b3b4+c3c4=0.2.空间角的计算(1)两条异面直线所成角的求法设直线a,b的方向向量为a,b,其夹角为θ,则cosφ=|cosθ|=|a·b||a||b|(其中φ为异面直线a,b所成的角).(2)直线和平面所成角的求法如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,两向量e与n的夹角为θ,则有sinφ=|cosθ|=|e·n||e||n|.(3)二面角的求法①利用向量求二面角的大小,可以不作出平面角,如图所示,〈m,n〉即为所求二面角的平面角.②对于易于建立空间直角坐标系的几何体,求二面角的大小时,可以利用这两个平面的法向量的夹角来求.如图所示,二面角α-l-β,平面α的法向量为n1,平面β的法向量为n2,〈n1,n2〉=θ,则二面角α-l-β的大小为θ或π-θ.分类突破一、利用向量证明平行与垂直例1如图所示,已知直三棱柱ABC—A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.求证:(1)DE∥平面ABC;(2)B1F⊥平面AEF.证明如图建立空间直角坐标系A—xyz,令AB=AA1=4,则A(0,0,0),E(0,4,2),F(2,2,0),B(4,0,0),B1(4,0,4).(1)取AB中点为N,连结CN,则N(2,0,0),C(0,4,0),D(2,0,2),∴DE→=(-2,4,0),NC→=(-2,4,0),∴DE→=NC→,∴DE∥NC,又 NC⊂平面ABC,DE⊄平面ABC.故DE∥平面ABC.(2)B1F→=(-2,2,-4),EF→=(2,-2,-2),AF→=(2,2,0).B1F→·EF→=(-2)×2+2×(-2)+(-4)×(-2)=0,B1F→·AF→=(-2)×2+2×2+(-4)×0=0.∴B1F→⊥EF→,B1F→⊥AF→,即B1F⊥EF,B1F⊥AF,又 AF∩FE=F,∴B1F⊥平面AEF.归纳拓展(1)证明线面平行须证明线线平行,只需证明这条直线与平面内的直线的方向向量平行.可用传统法也可用向量法,用向量法更为普遍.(2)证明线面垂直的方法:可用直线的方向向量与平面的法向量共线证明;也可用直线的方向向量与平面内两条相交直线的方向向量垂直证明.(3)证明面面垂直通常转化为证线面垂直,也可用两平面的法向量垂...