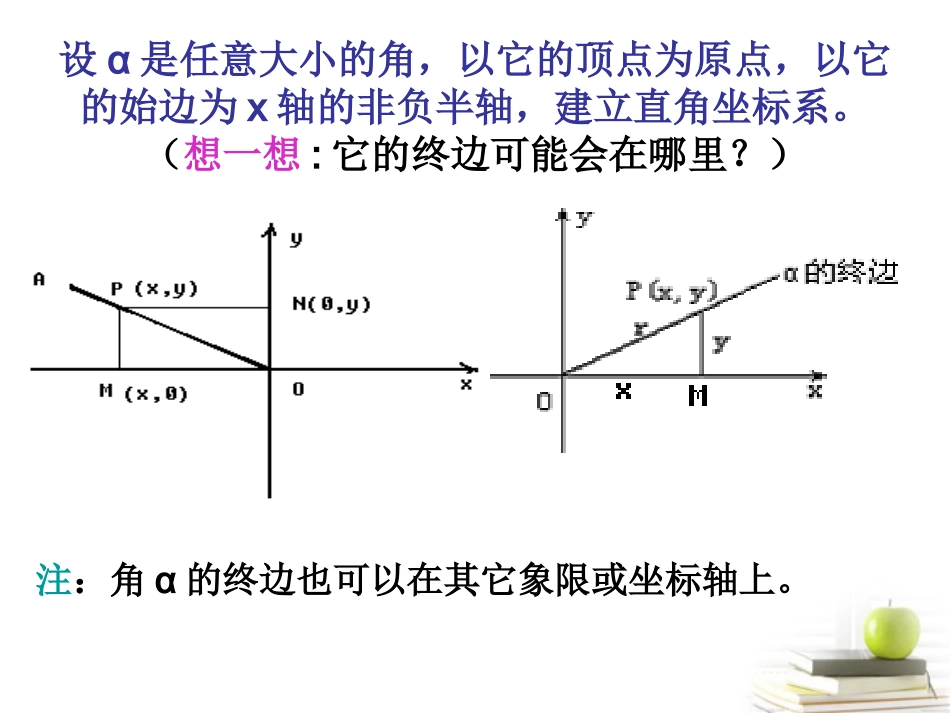
任意角的三角函数(一)1.锐角三角函数在Rt△ABC中,∠A是锐角,∠C是直角,则:想一想:如果现在把锐角A改成是任意大小的正角、负角或零角,那你觉得还能在直角三角形中求解吗?为什么?你有什么好的办法吗?设α是任意大小的角,以它的顶点为原点,以它的始边为x轴的非负半轴,建立直角坐标系。(想一想:它的终边可能会在哪里?)注:角α的终边也可以在其它象限或坐标轴上。想一想:(1)能不能用P点的坐标来表示α角的三角函数呢?在角α的终边上任取一点P(x,y),它到原点的距离为r(r>0)(2).如果把P点在α角终边上移动,那么,x、y、r是否随之改变?这三个比值是否也随之改变?为什么?由此可见,三个比值都是由角α完全决定,而与点p在α的终边上的位置无关。注意:其中点p不是原点,当角α的终边不在y轴上时,tanα才有意义!对应的函数分别叫做正弦函数、余弦函数、正切函数,统称为三角函数。2.任意角的三角函数yxoyxoyyyyxxxxrrrr3.概念辨析任意角的三角函数定义与锐角三角函数的定义,有什么区别和联系?联系:任意角的三角函数是锐角三角函数的推广;锐角三角函数是任意角的三角函数的特例。区别:锐角三角函数是以边长的比来定义的,都是正值;任意角的三角函数是以坐标与距离、坐标与坐标的比来定义的,不一定是正值。4、任意角的三角函数定义xyo●P(x,y)r的终边yxxryrxyrxrycot,sec,csctan,cos,sin22yxr{,}tanRcosRsin定义域三角函数2k)(Zk例1.已知角α的终边上一点p(-4,-3),分别求sinα,cosα,tanα.•演练反馈:已知角α的终边上一点p(-1,2),分别求sinα,cosα,tanα.例2.已知角α=,分别求sinα,cosα,tanα.34在直角坐标系中,我们称以原点O为圆心,以单位长度为半径的圆为单位圆(unitcircle).yxOABAOB的终边与单位圆的交点坐标为23,21)34sin()34cos()34tan(232131例3.已知角α=,分别求sinα,cosα,tanα.演练反馈:已知角α=/2,分别求sinα,cosα,tanα.yOAB1x你记住了吗?度弧度0003004506009001200135015001800270036006432233456322sincostan212333212332123321233312222122220101001001010yxo+-+++++-----yxoyxo全为+yxosincostancot记法:一全正二正弦三正切四余弦sinyrcosxrtanyx三角函数值在各象限的符号是怎样的?例4判断满足以下条件的角的终边所在的位置:①sinθ<0且tanθ>0②cosθ<0且tanθ<0③cosθ>0且sinθ<0④cosθ≤0且tanθ≥0.,tan)2tan(,cos)2cos(,sin)2sin(Zkkkk其中回答下列问题:1.角与角+2k的终边有何关系?2.角与角+2k的三角函数值有何关系?诱导公式一:公式的作用:可以把任意角的三角函数值分别转化为0到2的角的同一三角函数值.yxosincos+2k例5(1)确定下列三角函数值的符号:①cos2500tan②311③sin(-750°)④cos7()5(1).若sinα=1/3,且α的终边经过点p(—1,y),则α是第几象限的角?并求cosα,tanα的值。(2)下列四个命题中,正确的是A.终边相同的角都相等B.终边相同的角的三角函数相等C.第二象限的角比第一象限的角大D.终边相同的角的同名三角函数值相等232,44yr思考题1.若点p(-8,y)是角α终边上一点,且sinα=3/5,则y的值是__________.2.已知角α的终边经过点p(-4a,3a),(a≠0),求sinα,cosα,tanα.64.已知是第三象限角,求coscostantansinsin的值.5、设角属于第二象限角,且,则角属于第象限角?coscos222....ABCD一二三四C任意角的三角函数定义xyo●P(x,y)r的终边yxxryrxyrxrycot,sec,csctan,cos,sin22yxr小结{,}tanRcosRsin定义域三角函数2k)(Zk三角函数值的符号:“第一象限全为正,二正三切四余弦”sinxTanxcotxcosxtan)2tan(cos)2cos(sin)2sin(kkk诱导公式一诱导公式一小结•作业:P20A1、2、3、4、6、7