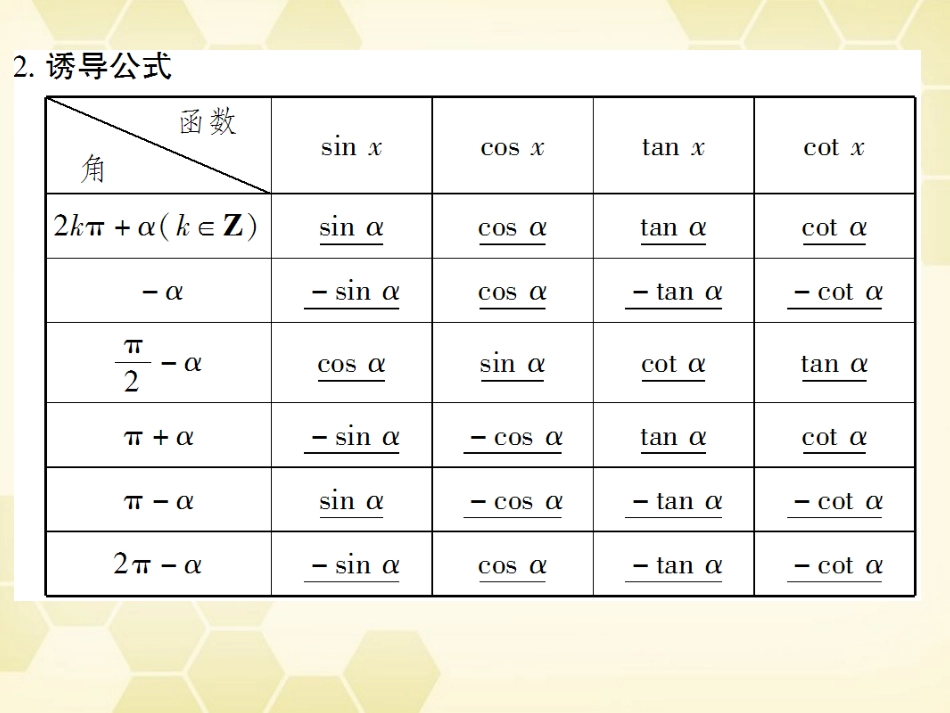
第2课时同角三角函数的基本关系与诱导公式答案:A答案:A答案:B1.在应用平方关系求角的三角函数值时,一定要先确定所在的象限,再进一步确定三角函数值的符号.2.已知角α的某一三角函数值,求角α的其余五种三角函数值时,要注意公式的合理选择,尽量多选用倒数、商数关系,少选用平方关系,在使用平方关系时一定要根据角α所在的象限确定符号.1“”“.应用诱导公式,重点是函数名称与正负”号的正确判断.求任意角的三角函数值的问题,都可以通过诱导公式化为锐角三角函数的求值问“”→“”→题,具体步骤为负角化正角正角化锐角求值.2.使用诱导公式要注意三角函数值在各个象限的符号,如果出现kπ±α的形式时,需要对k的值进行分类讨论,以确定三角函数值的符号.1.在利用同角三角函数的基本关系式进行求值、化简、证明时:(1)如果函数种类比较多,可考虑切化弦;(2)“要特别注意平方关系的使用,如1”的代换技巧和消去等.2.诱导公式的记忆“”“记忆口诀奇变偶不变,符号看象限,意思是说角±α,k∈Z”的三角函数值:当k为奇数时,正弦变余弦,余弦变正弦;当k为偶数时,函数名不变,然后α的三角函数值前面加上当视α为锐角时,原函数值的符号.3.利用诱导公式把任意角的三角函数转化为锐角三角函数的基本步骤是:通过对近三年高考试题的统计分析可以看出以下的命题规律:1.考查热点:同角三角函数的基本关系.2.考查形式:选择题、填空题和解答题均可能出现,但以客观题为主,属于低中档题目.3.考查角度:“”一是考查同角三角函数的基本关系,解题的关键是理解公式中同角的含义,明确公式成立的条件,掌握公式的变形形式.二是对诱导公式的考查,诱导公式作为一个应用广泛的工具,在求值、化简、证明题中经常利用它对式子进行化简.4.命题趋势:诱导公式在三角化简中的正用和逆用.答案:B[阅后报告]本题的难点一是确定k的正负,二是同角三角函数关系的转化.答案:B答案:D答案:B4.已知f(x)=asin(πx+α)+bcos(πx-β),其中α、β、a、b均为非零实数,若f(2010)=-1,则f(2011)等于()A.-1B.0C.1D.2解析:由诱导公式知f(2010)=asinα+bcosβ=-1,∴f(2011)=asin(π+α)+bcos(π-β)=-(asinα+bcosβ)=1.答案:C练规范、练技能、练速度