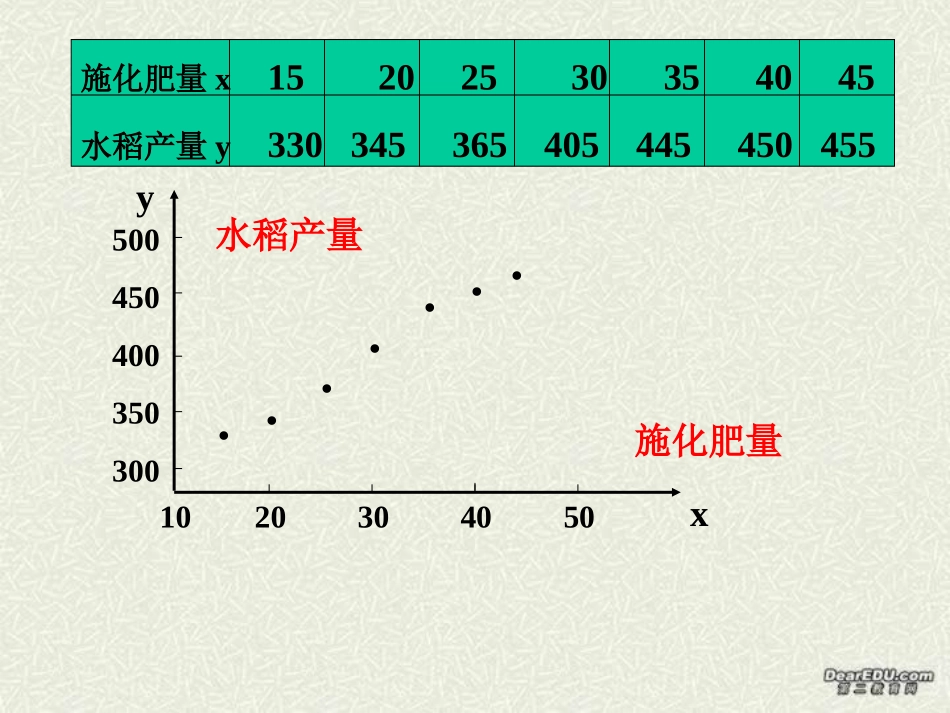
问题1:正方形的面积y与正方形的边长x之间的函数关系是y=x2确定性关系问题2:某水田水稻产量y与施肥量x之间是否有一个确定性的关系?例如:在7块并排、形状大小相同的试验田上进行施肥量对水稻产量影响的试验,得到如下所示的一组数据:施化肥量x15202530354045水稻产量y330345365405445450455复习、变量之间的两种关系1020304050500450400350300·······施化肥量x15202530354045水稻产量y330345365405445450455xy施化肥量水稻产量自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。1、定义:1):相关关系是一种不确定性关系;注对具有相关关系的两个变量进行统计分析的方法叫回归分析。2):2、现实生活中存在着大量的相关关系。如:人的身高与年龄;如:人的身高与年龄;产品的成本与生产数产品的成本与生产数量;量;商品的销售额与广告商品的销售额与广告费;费;家庭的支出与收入。家庭的支出与收入。等等等等探索:水稻产量y与施肥量x之间大致有何规律?1020304050500450400350300·······发现:图中各点,大致分布在某条直线附近。探索2:在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?施化肥量x15202530354045水稻产量y330345365405445450455xy散点图施化肥量水稻产量1020304050500450400350300·······xy施化肥量水稻产量yx21(,)(),niiiQyx取最小值时,的值推导过程请阅读P921、所求直线方程叫做回归直线方程;相应的直线叫做回归直线。2、对两个变量进行的线性分析叫做线性回归分析。2、回归直线方程:1122211()()ˆ,()ˆˆnniiiiiinniiiixxyyxnxybxxxnxaybxynn(x-x)(y-y)xy-nxyiiiii=1i=1ˆb==,nn222(x-x)x-nxiii=1i=1ˆˆa=y-bx.nn11x=x,y=y.iinni=1i=1其中最小二乘法:ˆˆˆybxa(,)xy称为样本点的中心。例题1从某大学中随机选出8名女大学生,其身高和体重数据如下表:编号12345678身高165165157170175165155170体重4857505464614359求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。1.散点图;2.回归方程:3.通过探究栏目引入“线性回归模型”。此处可以引导学生们体会函数模型与回归模型之间的差别。172.85849.0ˆxy分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.ˆ学身高172cm女大生体重y=0.849×172-85.712=60.316(kg)n(x-x)(y-y)iii=1r=nn22(x-x)(y-y)iii=1i=1相关系数r>0正相关;r<0负相关.通常,r>0.75,认为两个变量有很强的相关性.本例中,由上面公式r=0.798>0.75.探究?身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,其原因是什么?(1)由图形观察可以看出,样本点呈条状分布,身高和体重有比较好的线性相关关系,因此可以用线性回归方程刻画它们之间的关系。(2)从散点图还可以看到,样本点散布在某一条直线的附近,而不是一条直线上,所以不能用一次函数y=bx+a来描述它们之间的关系。这时我们用下面的线性回归模型来描述身高和体重的关系:y=bx+a+e其中a和b为模型的未知参数,e是y与之间的误差,通常e称为随机误差。ˆy2它的均值E(e)=0,方差D(e)=σ>0ˆy线性回归模型y=bx+a+e2E(e)=0,D(e)=σˆyy=bx+a+e其中a和b为模型的未知参数,e是y与之间的误差,通常e称为随机误差。思考?产生随机误差e的原因是什么?p96探究?为了衡量预报的精度,需要估计的σ2值?(1,2,....)ˆˆˆˆˆiiiiiiybxainyyybxaiiiii随机误差e其估计值为:ee称为相应点(x,y)的残差22111ˆˆˆˆ(,)(2)22ˆˆ(,)niieQabnnnQab类比样本方差估计总体方差的思想称为残差平方和21(,)()niiiQyx(1)根据散点图来粗略判断它们是否线性相关。(2)是否可以用线性回归模型来拟合数据(3)通过残差来判断模型拟合的效果这种分析工作称为残差分析1,2,3,,ˆˆˆˆ.....neeee