高一数学正弦、余弦函数图象的性质课件1 课件VIP免费

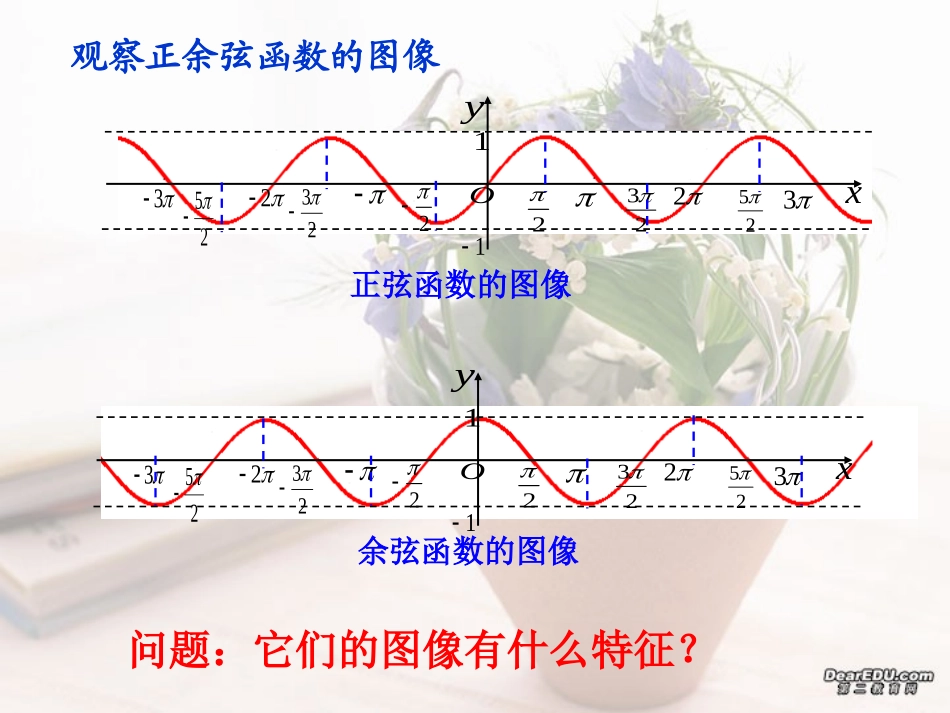
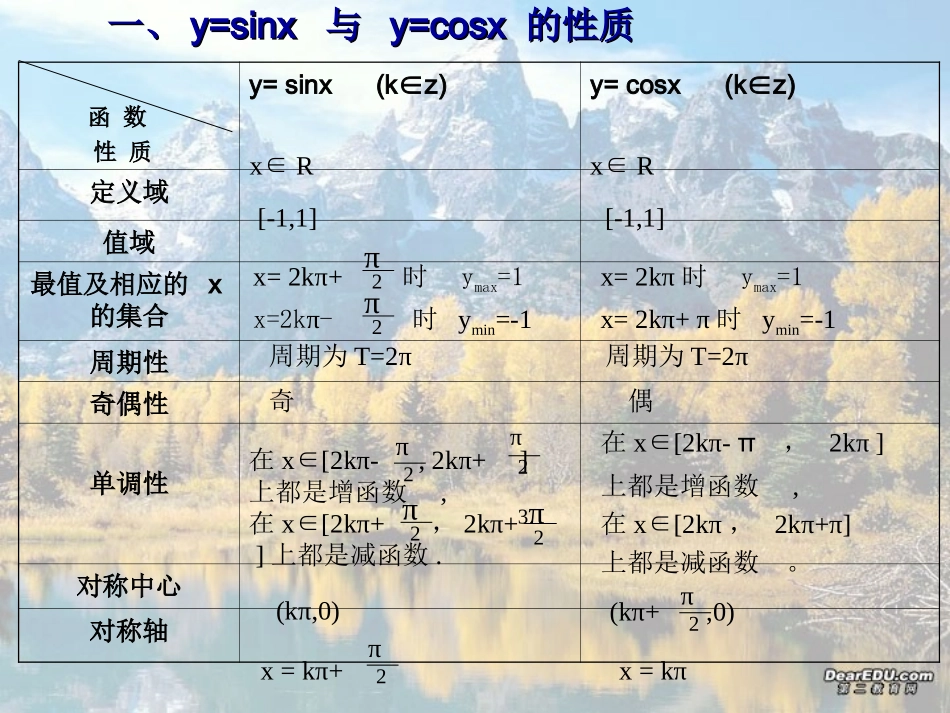
1.4.2正弦、余弦函数图象的性质x22322523yO23225311问题：它们的图像有什么特征？观察正余弦函数的图像正弦函数的图像余弦函数的图像x22322523yO23225311x=2kπ+时ymax=1x=2kπ-时ymin=-1π2π2函数性质y=sinx(kz)∈y=cosx(kz)∈定义域值域最值及相应的x的集合周期性奇偶性单调性对称中心对称轴x∈Rx∈R[-1,1][-1,1]x=2kπ时ymax=1x=2kπ+π时ymin=-1周期为T=2π周期为T=2π奇偶在x[2kπ-∈π，2kπ]上都是增函数,在x[2kπ∈，2kπ+π]上都是减函数。(kπ,0)x=kπ在x[2kπ-,2kπ+]∈上都是增函数,在x[2kπ+∈，2kπ+]上都是减函数.π2π2π23π2(kπ+,0)π2x=kπ+π2一、一、y=sinxy=sinx与与y=cosxy=cosx的性质的性质（1）三角函数图象的周期性[问题]7天后星期几？今天星期几？14天后呢？100天后呢？XX+2πyx024-2y=sinx(xR)∈三角函数的周期性自变量x增加2π时函数值不断重复地出现的oyx4π8πxoy6π12π问题能不能从正弦、余弦函数周期性归纳出一般函数的规律性？xy024-2y=sinx(xR)∈三角函数的周期性对于函数f(x)，如果存在一个非零常数Ｔ，使得当xx取定义域取定义域(D(D))内的每一个值内的每一个值时，都有f(x)＝f(x+T)，那么函数f(x)就叫做周期函数．非零常数T叫做这个函数的周期．周期函数的定义对于一个周期函数f(x),如果在它的所有正周期中存在一个最小的正数，那么这个最小的正数就叫做f(x)的最小正周期．正弦函数、余弦函数都是周期函数，2kπ(k∈Z且k≠0)是它们的周期，最小正周期是2π.xoy4π12π6π8π2π10πoyx4πy=sinx(x[0,4π])∈是周期函数吗？f(x)=1是周期函数吗？xy024-2(1)观察等式是否成立？如果成立，能不能说是y=sinx的周期？sin()sin2442(3)由诱导公式，是否可以说的周期为2π?xxcos(2)cos33xycos3(2)T(T≠0)是f(x)的周期，nT(nN∈+)是f(x)的周期？例2求下列函数的周期：(1)y=3cosx，xR∈(2)y=sin2x，xR∈Rx)6x21sin(2y)3(，2T0,0AA,Rx),xcos(AyRx),xsin(Ay的周期数，且中为常、、其函数及一般地，函数练习：课本P401，2X小结：1、一般地，对于函数f(x)，如果存在一个非零常数Ｔ，使得当x取定义域内的每一个值时，都有f(x)＝f(x+T)，那么函数f(x)就叫做周期函数．非零常数T叫做这个函数的周期．2、由周期函数的定义知：f(x+T)=f(x)的两端作用的是相同的对应法则f.3、函数y=Asin(ωx+Ψ),x∈R及函数y=Acos(ωx+Ψ),xR(∈其中A,ω,Ψ为常数，且A≠0,ω>0)的周期T=2π/ω.对周期函数的理解1对D内任意的x,都有f(x+T)=f(x)成立.其中x+T也必须在D内.因此判断一函数不是周期函数,只需举一个反例就可以了.判断函数是周期函数吗?)0(cosxxy不是2一个函数是周期函数,但它并不一定有最小正周期.例如:f(x)=a(a为常数)3设T是函数的周期,那么也是函数的周期.只要求T是不为0的常数,不要误认为T一定是的倍数.Rx),x(f)0,(kZkkT