高中数学 151152曲边梯形及汽车行驶的路程2课时)课件 新人教A版选修2-2 课件VIP免费

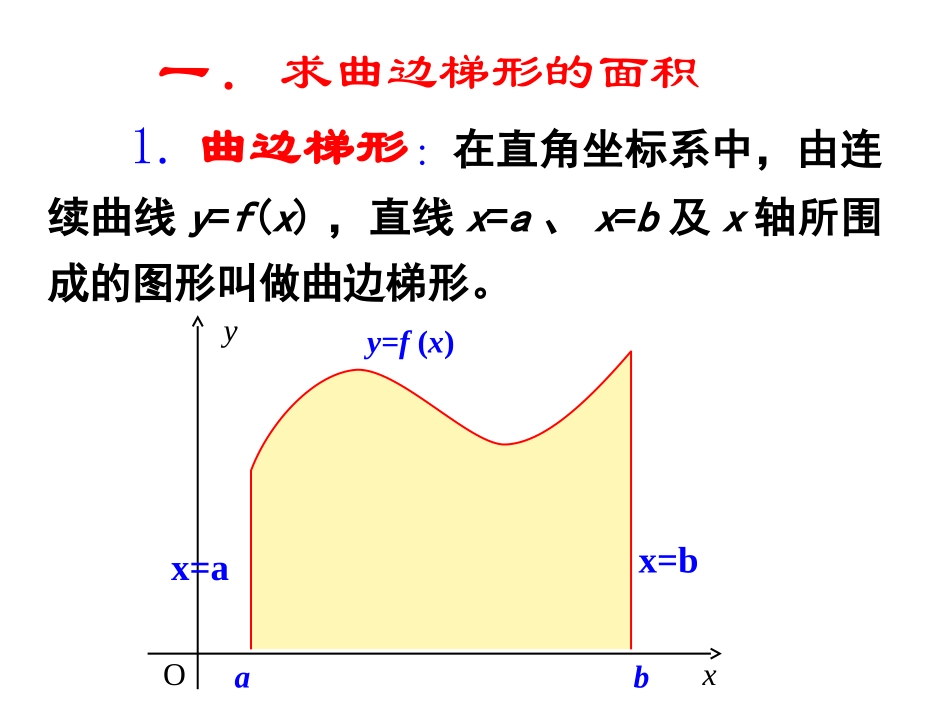
1.5定积分的概念一般地,如果函数y=f(x)在某个区间I上的图象是一条连续不断的曲线,那么就把它称为区间I上的连续函数.aboxyaboxy1.曲边梯形：在直角坐标系中，由连续曲线y=f(x)，直线x=a、x=b及x轴所围成的图形叫做曲边梯形。Oxyaby=f(x)一.求曲边梯形的面积x=ax=b因此，我们可以用这条直线L来代替点P附近的曲线，也就是说：在点P附近，曲线可以看作直线（即在很小范围内以直代曲）．P放大再放大PPy=f(x)baxyOA1AA1.用一个矩形的面积A1近似代替曲边梯形的面积A，得AA1+A2用两个矩形的面积近似代替曲边梯形的面积A，得y=f(x)baxyOA1A2AA1+A2+A3+A4用四个矩形的面积近似代替曲边梯形的面积A，得y=f(x)baxyOA1A2A3A4y=f(x)baxyOAA1+A2++An将曲边梯形分成n个小曲边梯形，并用小矩阵形的面积代替小曲边梯形的面积，于是曲边梯形的面积A近似为A1AiAn——以直代曲,无限逼近2．曲边梯形的面积求曲边梯形的面积即求下的面积)(xfy0)(xf——分成很窄的小曲边梯形，然后用矩形面积代后求和。若“梯形”很窄，可近似地用矩形面积代替在不很窄时怎么办？——以直代曲Oabxy)(xfyOabxy)(xfy例1.求抛物线y=x2、直线x=1和x轴所围成的曲边梯形的面积。n1n2nknn'211122222233111()()111211101(12(1))1(1)(21)611112.6nnnniiiiiiSSfxnnnnnnnnnnnnnnnnnnnxOy解:把底边[0,1]分成n等份,然后在每个分点作底边的垂线,这样曲边三角形被分成n个窄条,用矩形来近似代替,然后把这些小矩形的面积加起来,得到一个近似值:2xy因此,我们有理由相信,这个曲边三角形的面积为:lim111lim1261.3nnnSSnnn1n2nknnxy2xyOn1n2nknnxOy2xy小结:求由连续曲线yf(x)对应的曲边梯形面积的方法有理由相信，分点越来越密时，即分割越来越细时，矩形面积和的极限即为曲边形的面积。（1）分割（2）近似代替把这些矩形面积相加作为整个曲边形面积S的近似值。（4）取极限oxy(3)求和1.5.2汽车行驶的路程1SD2SD2()2vtt=-+Ovt12gggggg3SDjSDnSD1n2n3njn1nn-4SD1SD2SD2()2vtt=-+Ovt12gggggg3SDjSD1nS-D1n2n3njn1nnnn-01snD´11snD´31snD´11nsn-D´31snD´上图中:所有小矩形的面积之和,其极限就是由直线x=0,x=1和曲线v(t)=-t2+2所围成的曲边梯形的面积.