学案学案33平面向量的数量积平面向量的数量积返回目录1.平面向量的数量积已知两个非零向量a和b,则叫做a与b的数量积(或内积),记作.规定:零向量与任一向量的数量积为.两个非零向量a与b垂直的充要条件是,两个非零向量a与b平行的充要条件是.|a||b|·cos
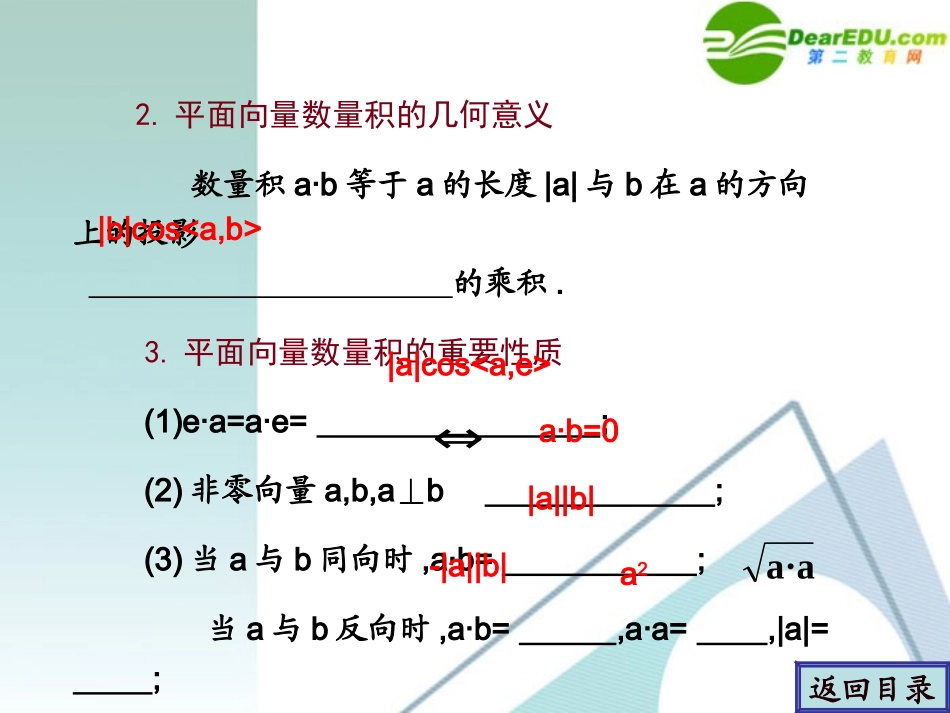
a·b=|a||b|·cos0a·b=0a·b=±|a||b|考点分析返回目录2.平面向量数量积的几何意义数量积a·b等于a的长度|a|与b在a的方向上的投影的乘积.3.平面向量数量积的重要性质(1)e·a=a·e=;(2)非零向量a,b,ab⊥;(3)当a与b同向时,a·b=;当a与b反向时,a·b=,a·a=,|a|=;|b|cos|a|cosa·b=0|a||b|-|a||b|a2a·a⇔返回目录(4)cosθ=;(5)|a·b||a||b|.4.平面向量数量积满足的运算律(1)a·b=(交换律);(2)(λa)·b==(λ为实数);(3)(a+b)·c=.≤|b||a|b•ab·aλa·ba·λba·c+b·c5.平面向量数量积有关性质的坐标表示设向量a=(x1,y1),b=(x2,y2),则a·b=,由此得到:若a=(x,y),则|a|2=或|a|=.(2)设A(x1,y1),B(x2,y2),则A,B两点间的距离|AB|=|AB|=.(3)设a=(x1,y1),b=(x2,y2),则ab⊥.返回目录x1x2+y1y2=0⇔x1x2+y1y2x2+y2y+x22221221)y-(y+)x-(x返回目录已知向量a=(cosx,sinx),b=(cos,-sin),且x∈〔-,〕.(1)求a·b及|a+b|;(2)若f(x)=a·b-|a+b|,求f(x)的最大值和最小值.考点一数量积的计算考点一数量积的计算23232x2x3π4π题型分析返回目录【解析】【解析】(1)a·b=cosxcos-sinxsin=cos2x,a+b=(cosx+cos,sinx–sin), x(),cosx>0,∈∴∴|a+b|=2︱cosx︱.【分析】【分析】利用数量积的坐标运算及性质即可求解,在求|a+b|时注意x的取值范围.23232x2x232x232x|,cosx|2=2cos2x+2=)2xsin-x23(sin+)2xcos+x23(cos=b+a2,3-π4π(2)由(1)可得f(x)=cos2x-2cosx=2cos2x-2cosx-1=2(cosx-)2-. x∈〔〕,≤cosx≤1,∴∴当cosx=时,f(x)取得最小值为-;当cosx=1时,f(x)取得最大值为-1.返回目录2123,3-π4π212123返回目录【评析】【评析】(1)与三角函数相结合考查向量的数量积的坐标运算及其应用是高考热点题型.解答此类问题,除了要熟练掌握向量数量积的坐标运算公式、向量模、夹角的坐标运算公式外,还应掌握三角恒等变换的相关知识.(2)求平面向量数量积的步骤:首先求a与b的夹角为θ,θ∈[0°,180°],再分别求|a|,|b|,然后再求数量积即a·b=|a||b|cosθ,若知道向量的坐标a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.*对应演练**对应演练*已知|a|=3,|b|=4,且a与b的夹角为θ=150°,求a·b,(a-b)2,|a+b|.a·b=|a|·|b|·cosθ=-6.(a-b)2=|a|2+|b|2-2a·b=25+12.|a+b|=返回目录33312-25=b+2a·b+a=b)+(a222返回目录设向量a,b,c满足a+b+c=0,(a-b)c,ab.⊥⊥若|a|=1,则|a|2+|b|2+|c|2的值是.【分析】【分析】由垂直的充要条件,寻找|a|,|b|,|c|之间的关系.考点二利用向量解决垂直问题考点二利用向量解决垂直问题【解析】【解析】 ab,b=-a-c,a·b=a·(-a-c)=-|a|⊥∴2-a·c=0,∴a·c=-|a|2=-1.又 (a-b)c,⊥∴(a-b)·c=0,a·c=b·c=-1.∴ a=-b-c,|a|∴2=|b|2+|c|2+2b·c,∴|b|2+|c|2=|a|2-2b·c=3,|a|∴2+|b|2+|c|2=4.返回目录【评析】【评析】垂直问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若a=(a1,a2),b=(b1,b2),则aba⊥1a2+b1b2=0,aba∥1b2-a2b1=0.⇔⇔返回目录*对应演练**对应演练*已知a=(cosα,sinα),b=(cosβ,sinβ)(0<α<β<π).(1)求证:a+b与a-b互相垂直;(2)若ka+b与a-kb的模相等,求β-α(其中k为非零实数).(1)证明:(a+b)·(a-b)=a2-b2=|a|2-|b|2=(cos2α+sin2α)-(cos2β+sin2β)=0,∴a+b与a-b互相垂直.(2)ka+b=(kcosα+cosβ,ksinα+sinβ),a-kb=(cosα-kcosβ,sinα-ksinβ),|ka+b|=,|a-kb|=. |ka+b|=|a-kb|,2kcos(β-α)=-2kcos(β-α).∴又k≠0,cos(β-α)=0.∴而0<α<β<π,β-α=.∴返回目录1+α)-2kcos(β+k22k+α)-2kcos(β-12π返回目录设两个向量e1,e2满足|e1|=2,|e2|=1,e1与e2的夹角为,若向量2te1+7e2与e1+te2的夹角为钝角,求实数t的范围.【分析】【分析】由公式cosθ=可得θ若为钝角,则cosθ<0,即a·b<0,从而可求出λ的取值范围,同时要...