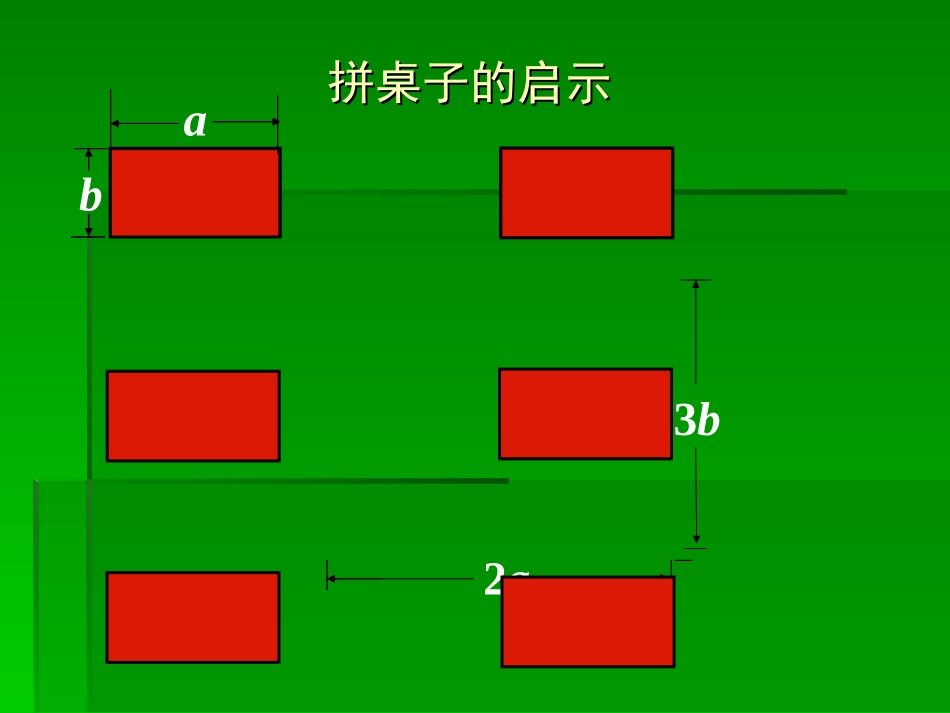
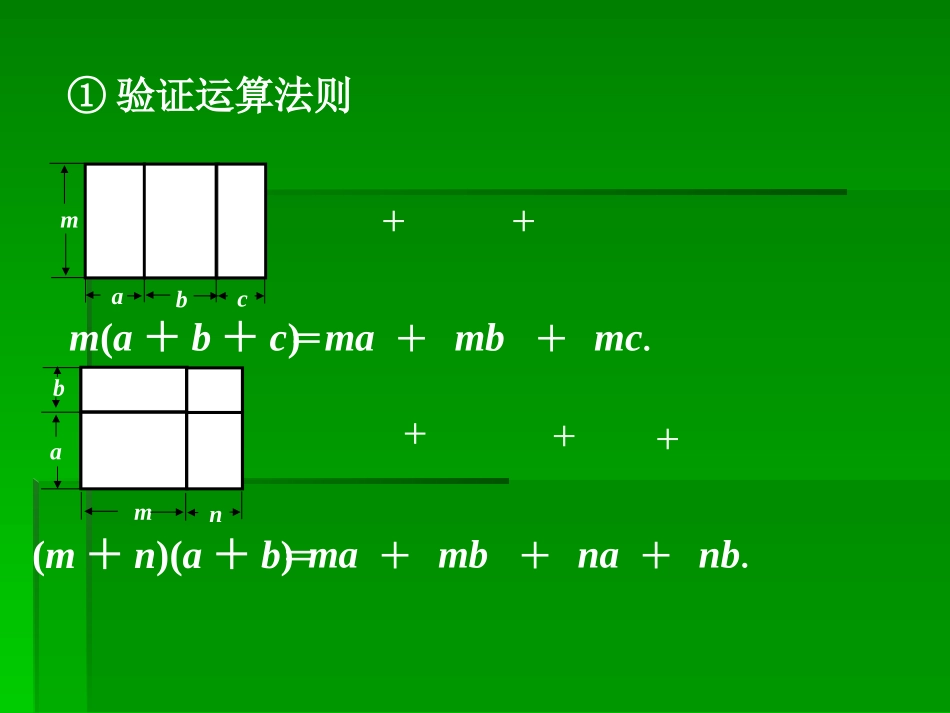
面积与代数恒等式面积与代数恒等式拼桌子的启示拼桌子的启示ab2a3bmacbabmn①验证运算法则+++++=m(a+b+c)ma+mb+mc.=(m+n)(a+b)ma+mb+na+nb.aabb②验证乘法公式abab(a+b)(a-b)a2b2-=(a+b)2+2aba2+b2=说一说(经典再现)说一说(经典再现)::从图形面积到代数恒式②验证乘法公式单项式乘以多项式法则多项式乘以多项式法则两数和乘以这两数差公式两数和的平方公式单项式乘以单项式法则①验证运算法则③验证根号2的存在④证明勾股定理④证明勾股定理ABCD边长为1的正方形的对角线长为2abc③验证的存在2112(a+b)2=化简得a2+b2=c2c2+4×ab21c下图是由四个完全相同的直角三角形拼出的正方形,你能用它来验证a2+b2=c2吗?用一用abc2=化简得a2+b2=c2+(b-a)24×ab21做一做做一做每四人为一个小组,用准备好的纸片任意拼每四人为一个小组,用准备好的纸片任意拼接出一些图形,用不同的方法来计算拼成图接出一些图形,用不同的方法来计算拼成图形的面积形的面积,,并写出一个代数恒等式并写出一个代数恒等式..拼出来拼出来以后小组里面共同分享一下,看哪个小组最以后小组里面共同分享一下,看哪个小组最多最快。多最快。议一议大家谈一谈在刚才的观察和实验中的体会大家谈一谈在刚才的观察和实验中的体会..从代数恒等式到图形面积从代数恒等式到图形面积做一做:做一做:请同学们用拼图的方法来验证下列代数恒等式的正请同学们用拼图的方法来验证下列代数恒等式的正确性?确性?(1)3(1)3aa·2·2bb==66abab(2)(2)aa22++abab==aa((aa++bb))(3)(2(3)(2aa++bb)()(aa++bb))==22aa22++33abab++bb22(4)((4)(aa++22bb)(2)(2aa--bb))==22aa22++33abab--22bb22(1)3(1)3aa·2·2bb=6=6abab(2)(2)aa22++abab==aa((aa++bb))(3)(2(3)(2aa++bb)()(aa++bb)=2)=2aa22+3+3abab++bb22(4)((4)(aa+2+2bb)(2)(2aa--bb)=2)=2aa22+3+3abab-2-2bb22ab3a2bbaaaaaababbabaabb议一议:议一议:通过刚才的拼图,大家认为根据代数恒等式来通过刚才的拼图,大家认为根据代数恒等式来拼图有什么技巧?拼图有什么技巧?例例11在在RtRt△△ABCABC中,∠中,∠CC==90°90°,,BBCC==33,,ACAC==44,求,求ABAB及及ABAB边上的边上的高高..CABD变式训练如图,在△变式训练如图,在△ABCABC中,中,ABAB==ACAC=5=5,,BCBC=6=6,点,点MM为为BCBC中点,中点,MNMN⊥⊥ACAC于点于点NN,,则则MNMN等于()等于()6595125165B.C.D.A.CABNM例例22如图,在长方形纸片如图,在长方形纸片ABCDABCD中,中,ADAD==44,,CDCD==33,沿,沿AEAE折叠纸片,使点折叠纸片,使点DD落在落在ACAC上的点上的点FF处,求处,求EFEF的长的长..ABCDEF这节课你学到了什么?这节课你学到了什么?11、用不同的方法来表示同一图形的面积可、用不同的方法来表示同一图形的面积可以得出代数恒等式;以得出代数恒等式;22、已知代数恒等式,能设计图形验证其正、已知代数恒等式,能设计图形验证其正确性;确性;33、学会了利用“数形结合”来解题。、学会了利用“数形结合”来解题。无题无题有数无形少直观,有形无数入微难有数无形少直观,有形无数入微难..数形结合无限好,割割补补尽开颜数形结合无限好,割割补补尽开颜..最新中考题欣赏最新中考题欣赏ACBPr1r2h(2009·内江市)(10分)阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连结AP,则S△ABP+S△ACP=S△ABC,即:AB·r1+AC·r2=AB·h,∴r1+r2=h(定值)(1)理解与应用:如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长。DCBAENFM212121(2)(2)类比与推理类比与推理如果把“等腰三角形”改成“等边三角形”,那么如果把“等腰三角形”改成“等边三角形”,那么PP的位的位置置可以由“在底边上任一点”放宽为“在三角形内任一点”,可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△即:已知等边△ABCABC内任意一点内任意一...