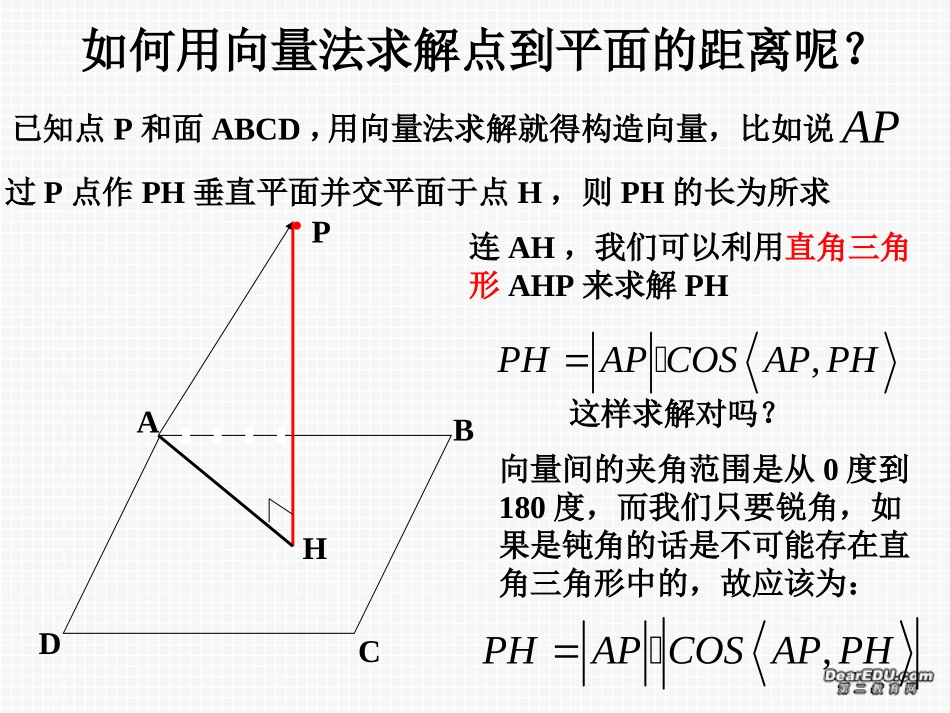
9.89.8距离距离用向量法求空间距离用向量法求空间距离上节课,我们学习了用立几的方法求距离,我们来简单回忆一下:点到平面的距离直线到与它平行平面的距离两个平行平面的距离异面直线的距离如何用向量法求解点到平面的距离呢?已知点P和面ABCD,ABCDP用向量法求解就得构造向量,比如说AP�H过P点作PH垂直平面并交平面于点H,则PH的长为所求连AH,我们可以利用直角三角形AHP来求解PH,PHAPCOSAPPH�,PHAPCOSAPPH�这样求解对吗?向量间的夹角范围是从0度到180度,而我们只要锐角,如果是钝角的话是不可能存在直角三角形中的,故应该为:ABCDHP,PHAPCOSAPPH�,APPH�可是怎么求呢?可以求解,可是呢?AP�PH�我们发现,垂直平面ABCD,我们可以理解成面ABCD的法向量PH�n,APPH�,APn�,,PHAPCOSAPPHAPCOSAPnAPnAPAPnAPnn������对点到距离的向量公式我们可以这样去理解:APnPHn�即点到平面的距离等于点和这个平面的任何一点所组成向量与此平面法向量的数量积的绝对值除于法向量的模,下面,我们用一个例题来理解一下,如何用向量来求点到平面的距离例题1:四面体SABC中,三角形ABC是等腰三角形,AB=BC=2a,SA=3a,角ABC为120度角,SA垂直面ABC,求点A到面SBC的距离这道题也是我们上一节课的例题,当时求解非常的麻烦,首先要找垂线,而找垂线我们要先找垂面,再做两垂直平面的垂线才找到,找到了垂线还要证明,证明完了还要通过一连串计算才把点到平面的距离求解出来,今天我们用向量法来求解,那么,我们来先想想步骤应该怎样:1:建立空间直角坐标系,并把相应点的坐标写出2:把公式中所需要的向量写出或求出3:套用公式xyz例题1:四面体SABC中,三角形ABC是等腰三角形,AB=BC=2a,SA=3a,角ABC为120度角,SA垂直面ABC,求点A到面SBC的距离SABC分析:我们首先要建立空间直角坐标系,建立坐标系,要使各个点的坐标简捷化,我们一般是观察有没有线面垂直的情况,有的话,那条线一般标为z轴,把面放在xoy的平面上,那么,请同学们思考,这道题应该怎么样来建立空间直角坐标系呢?以SA所在直线为z轴,以A为坐标原点建系接下来我们就来写出各点的坐标(0,0,0),(,3,0)(0,23,0),(0,0,3)ABaaCaSaxyzSABC3aBCAyx0120接下来我们要求面SBC的法向量了(,3,3),(0,23,3)(,,),,330,2330SBaaaSCaanxyznSBnSCaxayazayaz���一个平面的法向量有很多,只要满足上面的这个等式即可,为了计算的方便,我们通常会要相对简洁的数字组成的法向量,可以令z=1,则得到平面SBC的一个法向量了:33,,122nxyzSABC3a接下来我们要做些什么呢?求点A到面SBC任一点的向量,同样,也是数字越简洁越好(0,0,3)ASa�接下来我们套用公式了:33(0,0,3)(,,1)22322aASnadn�我们发现这样很快可以完成这道看似复杂无头绪的立几题,既然用向量法那么快能把点到面的距离求解出来,能不能把线面距离,面面距离,甚至是异面直线间的距离也转化成点面距离来求解呢?下面我们来看这么一道例题:例题2:已知在边长为的正中,E,F分别为BC和AC的中点,PA垂直面ABC,PA=2,设平面PFD过PF且与AE平行,交线段BC与点D,求AE与面PFD间的距离42ABC分析:这道题也是我们上一节课的例题,当时我们解决这道题时,是先找经过AE且垂直于面PFD的一个垂面,再在AE上找一点做两垂面交线的垂线,这条垂线就是AE到面PFD的距离,求解过程麻烦,今天,我们用向量来求解的话,我们应该怎么样把线面距离转化成点面距离呢?由题意可知,AE平行于面PFD,也就是说,AE上每一点到面PFD的距离都相等,那么我们可以转化成点A或点E或AE上任一点到面PFD的距离,这样,我们就可以用上一道例题的解题思路来进行解答了例题2:已知在边长为的正中,E,F分别为BC和AC的中点,PA垂直面ABC,PA=2,设平面PFD过PF且与AE平行,交线段BC与点D,求AE与面PFD间的距离42ABC首先,我们建立空间直角坐标系,以PA为z轴,A为坐标原点xyzAPBCEFD我们先把各点坐标写出,在求出面PFD的法向量,最后套用公式APndn�既然可以用向量法来解决点面,线面的距离,...