高一数学对数的概念课件北师大版 课件VIP免费

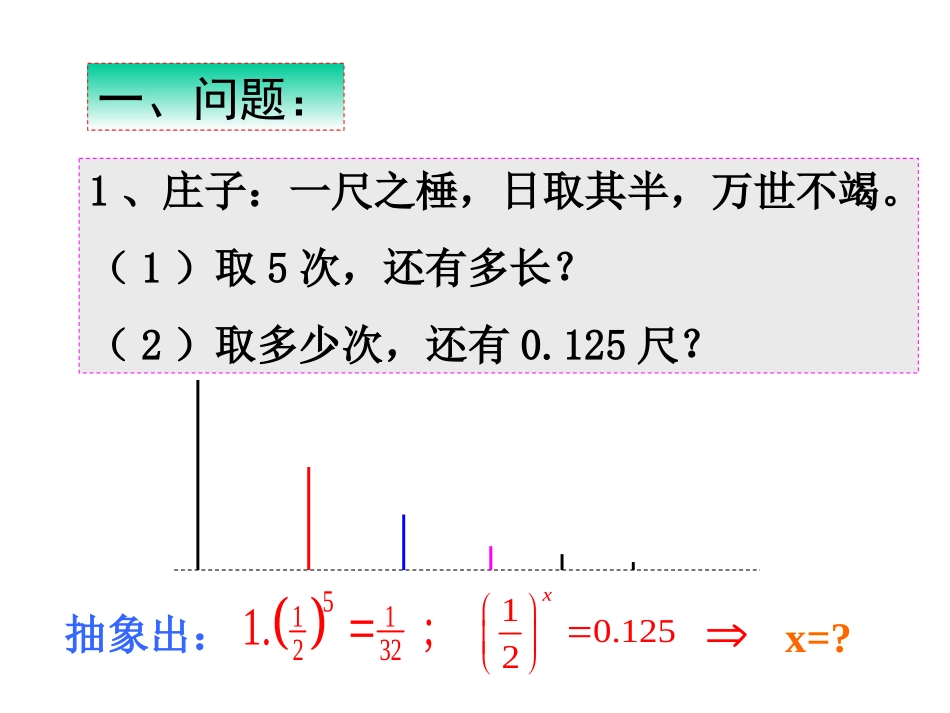
1、庄子：一尺之棰，日取其半，万世不竭。（1）取5次，还有多长？（2）取多少次，还有0.125尺？抽象出：5112321.;10.1252x一、问题：x=?2、假设2002年我国国民生产总值为a亿元，如果每年平均增长8%，那么经过多少年国民生产总值是2002年的2倍？抽象出：18%2xx=?1、对数的定义：一般地，如果a(a>0,a≠1)的b次幂等于N,就是ab=N那么数b叫做a为底N的对数，记作，a叫做对数的底数，N叫做真数。②.logbNaaNblogaN二、新授：①.注意底数的限制，a>0且a≠1;③.注意对数的书写格式．说明：底数对数真数幂指数底数↓↓↓↓↓↓logaN＝bab=N对数式与指数式的互化:logaNb例1:将下列指数式写成对数式：例2:将下列对数式写成指数式：431(1)216;(2)3;271(3)520;(4)()0.45;2ab51310(1)log1253;(2)log32;(3)log1.069.a例3:求下列各式的值：29(1)log64;(2)log27;①.为什么对数的定义中要求底数a>0且a≠1；②.是否是所有的实数都有对数呢？思考：底数对数真数幂指数底数↓↓↓↓↓↓logaN＝bab=N对数式与指数式的互化:①.为什么对数的定义中要求底数a>0且a≠1；②.是否是所有的实数都有对数呢？思考：底数对数真数幂指数底数↓↓↓↓↓↓logaN＝bab=N对数式与指数式的互化:负数和零没有对数；31(2)10;10000(4)1;(1)26.2=73.5167;(3)0.53=0.125;课堂练习将下列指数式写成对数式：①.常用对数（commonlogarithm）：以10为底的对数log10N,②.自然对数（naturallogarithm）：以无理数e=2.71828…为底的对数的对数logeN;两个重要对数：简记为:lgN.简记为:lnN.(在科学技术中,常常使用以e为底的对数)2(1)log62.5850;3(2)log0.80.2031;(3)lg30.4771;(4)ln31.0986;课堂练习将下列对数式写成指数式：求下列各式的值：探索与发现：(1)log31=0(2)lg1=00(3)log0.51=0(4)ln1=你发现了什么?“1”的对数等于零,即loga1=o求下列各式的值：探索与发现：(1)log33=1(2)lg10=11(3)log0.50.5=1(4)lne=你发现了什么?底数的对数等于“1”,即logaa=1求下列各式的值：探索与发现：你发现了什么?2log3(1)27log0.6(2)70.4log89(3)0.430.689logaNaN对数恒等式：求下列各式的值：探索与发现：你发现了什么?对数恒等式：lognaan43(1)log350.9(2)log0.98(3)lne458对数的基本性质1.负数和零没有对数；2.“1”的对数等于零,即loga1=o3.底数的对数等于“1”,即logaa=14.logaNaN对数恒等式：5.对数恒等式：lognaan思考(1)已知x满足等式532log[log(log)]0,.x16求logx的值(2)求值：2.51log6.25lgln100e(3)已知log2,log3,.aaxy3x+2y求a的值22932log5log32log512log42233(4)求下列各式的值思考题:小结三、归纳小结，强化思想1、引入对数的必要性；2、指数与对数的关系；3、对数的基本性质．