高考数学一轮复习 5.4 三角函数的性质课件 新课标 课件VIP免费

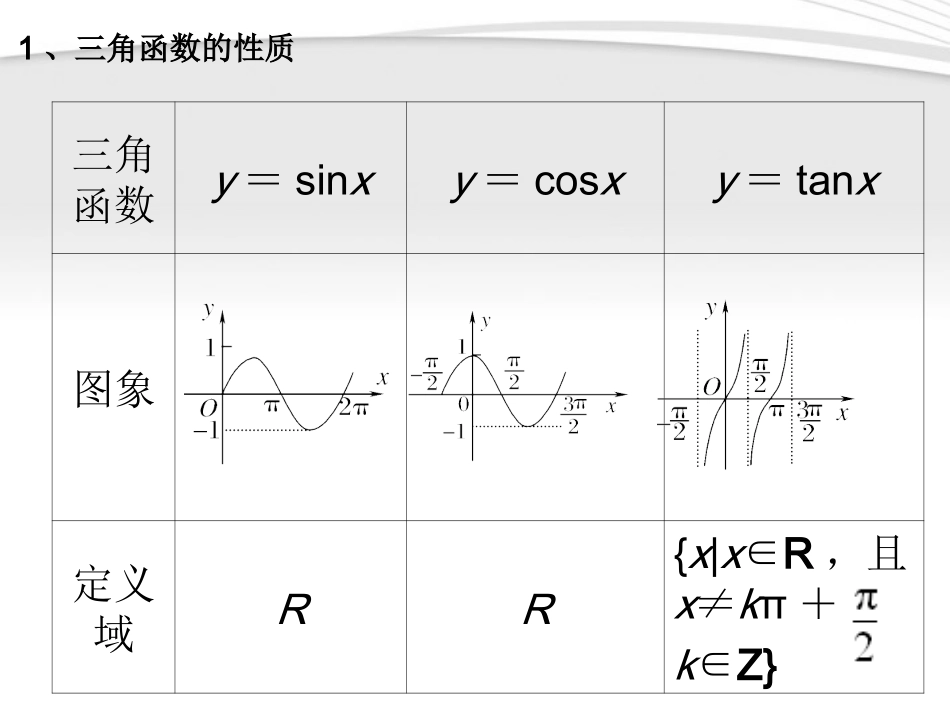
4.三角函数的性质三角函数y＝sinxy＝cosxy＝tanx图象定义域RR{x|x∈R，且x≠kπ＋k∈Z}1、三角函数的性质函数y＝sinxy＝cosxy＝tanx值域和最值[－1,1]，当x=2kπ－(k∈Z)时，ymin＝－1，当x＝2kπ＋(k∈Z)时，ymax＝1[－1,1]，当x＝2kπ时(k∈Z)，ymax＝1，当x＝2kπ＋π时(k∈Z)，ymin＝－1R，无最大值和最小值周期2π2ππ奇偶性奇偶奇对称性对称中心(kπ,0)k∈Z对称轴x＝kπ＋k∈Z对称中心(kπ＋，0)，k∈Z对称轴x＝kπk∈Z对称中心(,0)k∈Z无对称轴单调区间增区间[2kπ－，2kπ＋]减区间[2kπ＋，2kπ＋](k∈Z)减区间[2kπ，2kπ＋π]增区间[2kπ－π，2kπ](k∈Z)在(kπ－，kπ＋)(k∈Z)上是增函数2、思想方法:（1）总是用图象得函数的各性质,（2）选取一个恰当的周期讨论性质从而加上周期推广到整个定义域。（3）在研究函数)sin(xAy的各项性质的时候总是设ux从而只需讨论uysin的各项性质就可得到)sin(xAy的各项性质和由u的范围得到x的范围.（4）合一变形：y=asinx+bcosx=22ab)sin(x2222cossinaabbab这里，例1求下列函数的定义域题型一：三角函数的定义域题型二：三角函数的值域例2求下列函数的值域：(1)y＝sinx＋cosx(|x|≤)；(2)y＝cos2x＋2sinx(|x|≤)；(3)y＝sin2x＋2sinxcosx＋3cos2x.点评：求三角函数值域常用的方法．(1)将所给的三角函数转化为二次函数，通过配方法求值域，例如转化成y＝asin2x＋bsinx＋c型的值域问题．(2)化为一角一函形式求．(3)利用sinx、cosx的有界性求值域．(4)换元法．利用换元法求三角函数的值域，要注意元前后的等价性，不能只进行换元，不注意其等价性．(5)数形结合.例3(2011浙江六校第二次模拟)ω是正实数，如果函数f(x)＝2sinωx在[]上是增函数，那么ω的取值范围是________．题型三：三角函数的单调性例4.已知函数y＝2sin(ωx＋θ)为偶函数(0＜θ＜π)，其图象与直线y＝2的交点的横坐标为x1、x2，若|x1－x2|的最小值为π，则ω＝________，θ＝________.解析：y＝2sin(ωx＋θ)为偶函数且0＜θ＜π，∴θ＝，y＝2cosωx，y[∈－2,2]∴y＝2与y＝2cosωx交点为最高点由题设条件知，最小正周期为π∴＝π，∴ω＝2.故填2，.题型四：三角函数的周期性题型五：三角函数的奇偶性例5.(理)(2010·陕西)已知函数f(x)＝.(1)求函数f(x)的最小正周期及最值；(2)令g(x)＝f(x＋)，判断函数g(x)的奇偶性，并说明理由．3题型六：三角函数对称性问题例6.（1）(2011福州模拟冲刺)下列坐标所表示的点不是函数)62tan(xy的图象的对称中心的是（）（A）0,30,350,34（B）（C）（D）0,32(2)如果函数sin2cos2yxax的图象关于直线8x对称，则a作业：22()sin2sincos3cosfxxxxxxR()fxx()fx1.已知函数，(I)函数的最大值及取得最大值的自变量(II)函数的单调增区间．求:的集合；22sincos1sinxxyx23sinlog3sinxyx1sin3cosxyx2、求下列函数的值域：（1）；（2）（3）2385cossin2axaxy2,03.是否存在实数a，使得函数在闭区间a值？若不存在，试说明理由．上的最大值是1？若存在，求出对应的