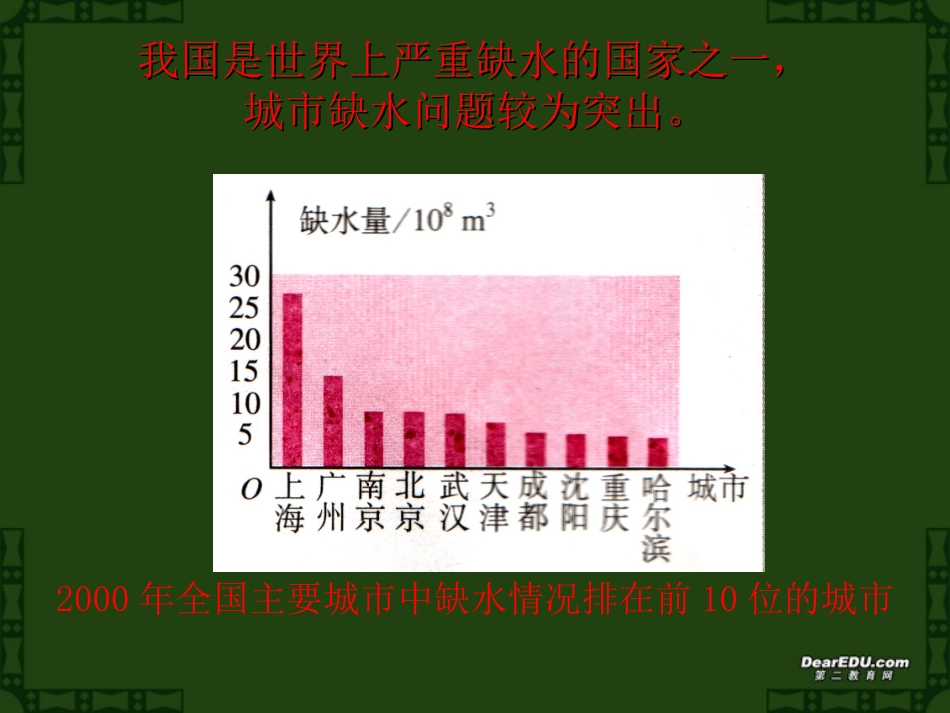
用样本的频率分布估计总体分布用样本的频率分布估计总体分布单位:河东三中学科:数学我国是世界上严重缺水的国家之一,我国是世界上严重缺水的国家之一,城市缺水问题较为突出。城市缺水问题较为突出。2000年全国主要城市中缺水情况排在前10位的城市某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超过a的部分按议价收费。①如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合理呢?②为了较合理地确定这个标准,你认为需要做哪些工作?思考:由上表,大家可以得到什么信息?通过抽样,我们获得了100位居民某年的月均用水量(单位:t),如下表:1.求极差:步骤:频率分布直方图2.决定组距与组数:组数=4.3-0.2=4.14.10.5=8.2组距极差=3.将数据分组[0,0.5),[0.5,1)…,,[4,4.5]4.列频率分布表100位居民月均用水量的频率分布表频率/组距月均用水量/t0.500.400.300.200.1000.511.522.533.544.55.画频率分布直方图探究:同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图的形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断。分别以1和0.1为组距重新作图,然后谈谈你对图的印象。练习:从一种零件中抽取了80件,尺寸数据表示如下(单位:cm):这里用x×n表示有n件尺寸为x的零件,如362.51×1表示有1件尺寸为362.51cm的零件。作出样本的频率分布表和频率分布直方图。小结:思考:如果当地政府希望使85%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量标准提出建议吗?频率分布直方图应用步骤1.求极差2.决定组距与组数3.将数据分组4.列频率分布表5.画频率分布直方图