高中数学 第三章本章优化总结课件 苏教版必修5 课件VIP免费

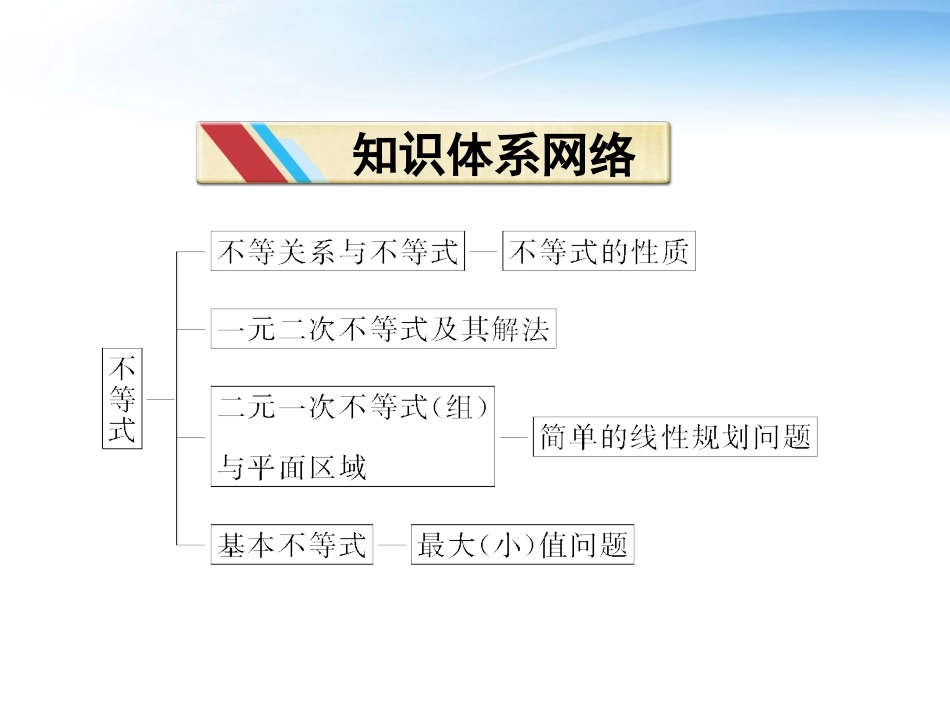
本章优化总结知识体系网络专题探究精讲专题一专题一不等式与函数、方程、数列的综合问题1．利用不等式的性质、不等式的证明方法、解不等式等知识可以解决函数中的有关问题，主要体现在：利用不等式求函数的定义域、值域、最值、证明单调性等．2．利用函数、方程、不等式之间的关系，可解决一元二次方程根的分布问题．3．不等式与数列的综合题经常出现在高考压轴题中，主要体现在比较数列中两项的大小等．例例11m为何值时，关于x的方程8x2－(m－1)x＋(m－7)＝0的两根：(1)为正根；(2)为异号根且负根绝对值大于正根；(3)都大于1；(4)一根大于2，一根小于2.【分析】本题看似考查二次方程根的问题，细看是考查不等式问题，再分析可见是考查三个“二次”(即一元二次方程、一元二次不等式、二次函数)的问题，找出这一本质是解决本题的关键．【解】设方程两根为x1，x2，则(1)Δ≥0，x1＋x2＞0，x1x2＞0，即[－m－1]2－4×8×m－7≥0，－－m－18＞0，m－78＞0.解得7＜m≤9或m≥25.(2)Δ＞0，x1＋x2＜0，x1x2＜0，即[－m－1]2－4×8×m－7＞0，－－m－18＜0，m－78＜0.解得m＜1.(3)Δ≥0，x1＋x2＞2，x1－1x2－1＞0.解得m≥25.(4)Δ＞0，x1－2x2－2＜0.解得m＞27.【点评】三个“二次”之间的关系是实现它们之间相互转化的桥梁．联系三个“二次”的纽带是二次函数的图象，利用图象的形象直观可以准确把握三个“二次”之间的关系，牢固地记忆相关结论．同时，在分析、解决具体问题时，利用二次函数图象可以帮助我们迅速找到解题方法．例例22正数数列{an}的前n项的和Sn满足2Sn＝an＋1，试求：(1)数列{an}的通项公式；(2)设bn＝1anan＋1，数列{bn}的前n项的和为Bn，求证：Bn＜12.【分析】应先求和再放缩．【解】(1)由已知得4Sn＝(an＋1)2，n≥2时，4Sn－1＝(an－1＋1)2，作差得：4an＝a2n＋2an－a2n－1－2an－1，所以(an＋an－1)(an－an－1－2)＝0.又因为{an}为正数数列，所以an－an－1＝2，即{an}是公差为2的等差数列，由2S1＝a1＋1，得a1＝1，所以an＝2n－1.即数列{an}的通项公式为an＝2n－1.(2)证明：bn＝1anan＋1＝12n－12n＋1＝12(12n－1－12n＋1)，所以Bn＝12(1－13＋13－15＋…＋12n－1－12n＋1)＝12－122n＋1＜12.【点评】如果数列的前n项和能直接求和或者通过变形后求和，则采用先求和再放缩的方法来证明不等式．求和的方式一般要用到等差、等比数列前n项和公式，或者利用分组、裂项、倒序相加等方法．专题二专题二不等式恒成立问题对于不等式恒成立求参数范围问题的常见类型及解法有以下几种1．变更主元法：根据实际情况的需要确定合适的主元，一般知道取值范围的变量要看作主元．2．分离参数法：若f(a)＜g(x)恒成立，则f(a)＜g(x)min.若f(a)＞g(x)恒成立，则f(a)＞g(x)max.3．数形结合法：利用不等式与函数的关系，将恒成立问题通过函数图象直观化．例例33设f(x)＝mx2－mx－6＋m，(1)若对于m∈[－2,2]，f(x)＜0恒成立，求实数x的取值范围．(2)若对于x∈[1,3]，f(x)＜0恒成立，求实数m的取值范围．【分析】(1)知道m的范围，所以应用变更主元法；(2)应用分离参数法．【解】(1)依题意，设g(m)＝(x2－x＋1)m－6，则g(m)为关于m的一次函数，且一次项系数x2－x＋1＝(x－12)2＋34＞0，∴g(m)在[－2,2]上递增，∴欲使f(x)＜0恒成立，需g(m)max＝g(2)＝2(x2－x＋1)－6＜0，解得：－1＜x＜2.(2)要使f(x)＝m(x2－x＋1)－6＜0在[1,3]上恒成立，则有m＜6x2－x＋1在[1,3]上恒成立，而当x∈[1,3]时，6x2－x＋1＝6x－122＋34≥69－3＋1＝67，∴m＜6x2－x＋1min＝67，∴m＜67.专题三专题三解含参数的不等式解含参数的不等式，解答过程中的不确定因素常需进行分类讨论，如一元二次不等式的二次项系数含参数时分系数等于0、不等于0两类讨论；不等式两边同乘以(或除以)一个数时，要讨论这个数的符号；一元二次不等式对应方程根的情况不定或有实根但大小不定时要讨论．例例44解关于x的不等式ax2＋ax－1＜0.(*)【分析】当a≠0时，不等式(*)为二次不等式，解二次不等式的关键是看二次...