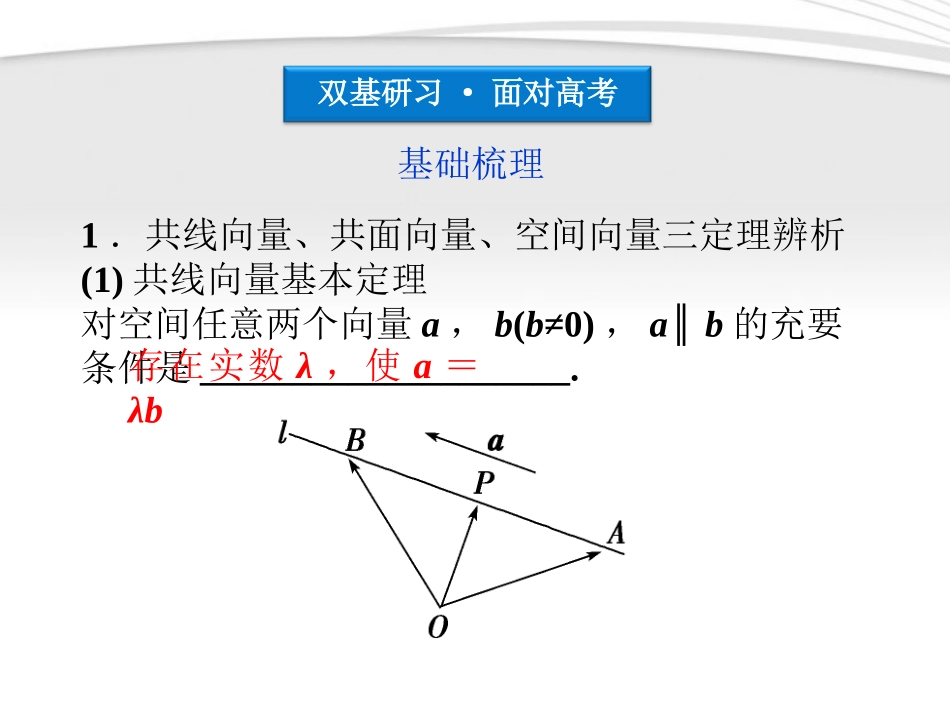
§9.4空间向量及其运算(B)考点探究·挑战高考考向瞭望·把脉高考9.4空间向量及其运算(B)双基研习·面对高考双基研习·面对高考基础梳理1.共线向量、共面向量、空间向量三定理辨析(1)共线向量基本定理对空间任意两个向量a,b(b≠0),a∥b的充要条件是____________________.存在实数λ,使a=λb推论:如果l为经过已知点A且平行于已知非零向量a的直线,那么对任一点O,点P在直线l上的充要条件是存在实数t,满足等式OP→=OA→+ta,其中向量a叫做直线l的方向向量,如图.线段AB的中点公式为(其中P是AB的中点)OP→=12(OA→+OB→).(2)共面向量基本定理如果两个向量a,b不共线,则向量p与向量a、b共面的充要条件是存在实数对x,y使____________.推论1空间一点P位于平面MAB内的充分必要条件是存在有序实数对x,y,使MP→=xMA→+yMB→,或对空间任一定点O,有OP→=OM→+xMA→+yMB→.①在平面MAB内,点P对应的实数对(x,y)是唯一的,①式叫做平面MAB的向量表示式.p=xa+yb推论2对空间任一点O和不共线的三点A、B、C,满足向量关系式OP→=xOA→+yOB→+zOC→(其中x+y+z=1)的四点P、A、B、C共面(当且仅当x+y+z=1时).(3)空间向量基本定理如果三个向量a,b,c不共面,那么对空间任一向量p,存在一个唯一的有序实数组x,y,z,使_________________.p=xa+yb+zc如果三个向量a,b,c不共面,那么所有空间向量所组成的集合就是{p|p=xa+yb+zc,x、y、z∈R},这个集合可看作是由向量a、b、c生成的,所以我们把_________叫做空间的一个基底,a,b,c都叫做基向量,(x,y,z)叫做p对基底{a,b,c}下的坐标.推论:设O、A、B、C是不共面的四点,则对空间任一点P,都存在唯一的三个序数x,y,z,使OP→=xOA→+yOB→+zOC→.{a,b,c}2.两向量的数量积(1)空间两个向量的夹角如图,已知两个非零向量a、b,在空间任取一点O,作OA→=a,OB→=b,则∠AOB叫做向量a与b的夹角,记作〈a,b〉.0≤〈a,b〉≤π,并且〈a,b〉=〈b,a〉.(2)若〈a,b〉=π2,则称a与b互相垂直,并记作a⊥b.(3)已知空间两个向量a,b,则|a||b|cos〈a,b〉叫做向量a,b的数量积,记作a·b,即a·b=__________________.(4)已知向量AB→=a和轴l,e是l上与l同方向的单位向量(如图).作点A在l上的射影A′,作点B在l上的射影B′,则A′B′→叫做向量AB→在轴l上或在e方向上的正射影,简称射影,可以证明A′B′→=|AB→|cos〈a,e〉=a·e.|a||b|cos〈a,b〉(5)性质①a·e=|a|cos〈a,e〉.②a⊥b⇔a·b=0.③|a|2=a·a.④cos〈a,b〉=a·b|a|·|b|.(6)运算律①(λa)·b=_________.②a·b=b·a(交换律).③a·(b+c)=a·b+a·c(分配律).λ(a·b)3.空间直角坐标系(1)空间直角坐标系在空间选定一点O和一个单位正交基底{i,j,k},以O为原点,分别以i,j,k的方向为正方向建立三条数轴:x轴,y轴,z轴,它们都叫做坐标轴.这时我们说建立了一个空间直角坐标系O-xyz,点O叫做原点,向量i,j,k叫做__________,通过每两个坐标轴的平面叫做坐标平面.坐标向量(2)坐标在空间直角坐标系O-xyz中,对空间任一点A,对应一个向量OA→,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使________________,则数组(x,y,z)叫做点A在此空间直角坐标系中的坐标.OA→=xi+yj+zk(3)空间向量的坐标运算设a=(a1,a2,a3),b=(b1,b2,b3),则a+b=_________________________;a-b=______________________;λa=______________________;a·b=______________________;a∥b⇔a1=λb1,a2=λb2,a3=λb3(λ∈R);a⊥b⇔______________________.(a1+b1,a2+b2,a3+b3)(a1-b1,a2-b2,a3-b3)(λa1,λa2,λa3)(λ∈R)a1b1+a2b2+a3b3a1b1+a2b2+a3b3=0提示:不是.向量平行于平面是指向量所在直线平行于平面α或在平面α内两种情况.因此,在用共面向量定理证明线面平行时,必须说明向量所在的直线不在平面内.1.向量AB→∥平面α与直线AB∥平面α是同一概念吗?思考感悟2.在空间直角坐标系中:P(x,y,z)关于x轴、y轴、z轴的对称点如何?P(x,y,z)关于原点的对称点如何?P(x,y...