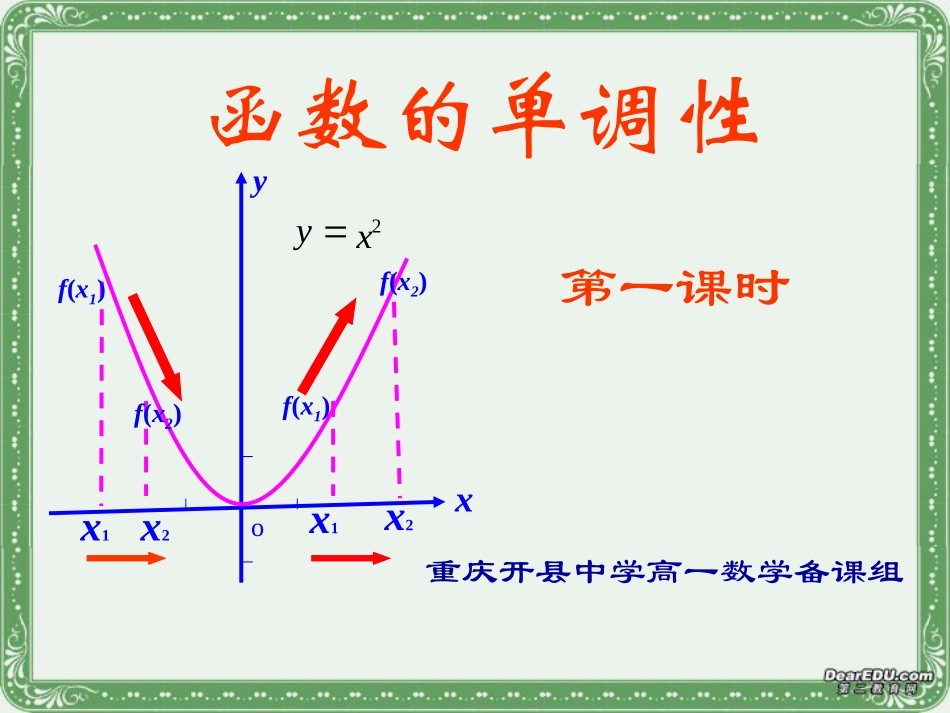
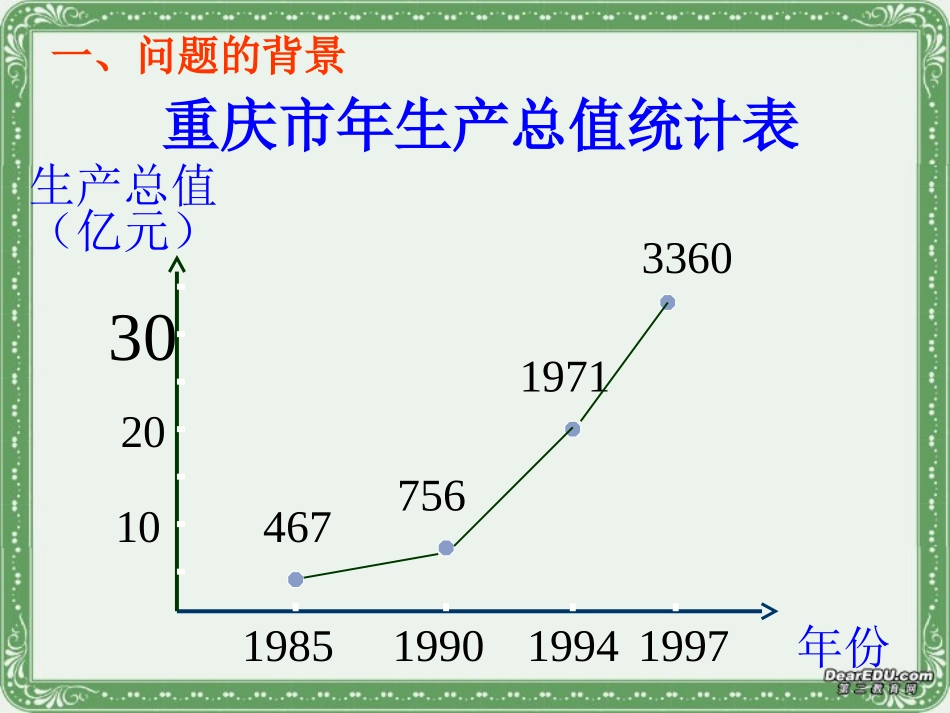
函数的单调性第一课时重庆开县中学高一数学备课组2xyoxyx2f(x2)x1f(x1)x1f(x1)x2f(x2)重庆市年生产总值统计表198519901994199746775619713360102030年份生产总值(亿元)一、问题的背景重庆市日平均出生人数统计表4233592091761985199019941997450150年份人数(人)2503502xyoxyx2f(x2)x1f(x1)x1f(x1)x2f(x2)当0f(x2),f(x)在(-∞,0)上是减函数f(x)在(0,+∞)上是增函数对函数单调性的理解:2、定义中x1、x2必须满足以下三点:①x1、x2是在同一个区间上②任意的两个实数,③设出了一大一小。1、函数的单调性是对定义域的某个区间而言的。同一函数在定义域内的不同区间上可能有不同的单调性.例如:y=x2在(-∞,0)上为减函数,在(0,+∞)上为增数;在(-∞,+∞)上就不具备单调性。例1下图是定义在闭区间[-5,5]上的函数的图象,根据图象说出的单调区间,以及在每一区间上,是增函数还是减函数.)(xfy)(xfy)(xfy-212345-23-3-4-5-1-112xyO三、例题讲解:解:根据函数图象可知在区间[-2,1),[3,5]上是增函数。函数y=f(x)单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中y=f(x)在区间[-5,-2),[1,3)上是减函数,x-212345-23-3-4-5-1-112y0例2、证明函数y=-x3+1在R上是减函数。用定义证明函数单调性的步骤:(1)取值.(2)作差变形.(因式分解,配方,有理化)(3)定号.(4)判断得结论.例3、已知函数f(x)=-(x-1)2(1)证明f(x)在(-∞,1]上是增函数(2)证明f(x)在(-∞,+∞)上不具有单调性小结1、写出常见函数的单调区间并指明是增区间还是减区间),0(),0,(,0a),0(),0,(,0a单减区间是时单减区间是时),(,0a),(,0a单减区间是时单增区间是时),a2b[],a2b,(,0a),a2b[],a2b,(,0a单减区间是单增区间是时单增区间是单减区间是时2、函数y=ax+b(a≠0)的单调区间是3、函数y=ax2+bx+c(a≠0)的单调区间是1、函数的单调区间是)(0axay四、课堂探究:小结的单调区间。)(、试求x1xxf2?)0axaxxf:的单调区间又如何呢()(函数推广五、课时小结1、理解函数单调性的定义2、能够掌握用定义法证明函数的单调性用定义证明函数单调性的步骤:(1)取值.(2)作差变形.(因式分解,配方,有理化)(3)定号.(4)判断得结论.)上是增函数。,)在区间((证明,其中)(、设函数0xf1aax1xxf324、若函数f(x)=x+2(a-1)x+2在区间[4,+∞)上是增函数,则实数a的取值范围是()5aD3aC3aB3aA、,、,、,、5、设f(x)是定义在区间U上的增函数,且f(x)>0,则下列函数中增函数的个数是())())(()()())(()(xfy4xfy3xf1y2xf1y12A、1B、2C、3D、4二、增、减函数的定义yOx)x(fy)x(f22x1x)x(f1)x(f1)x(f2)x(fyOx1x2x一般地,设函数y=f(x)的定义域为I,区间D⊆I对任意的x1D∈、x2D∈且x1f(x2),则称f(x)在区间D上是减函数,区间D称为y=f(x)的单调递减区间(2)在单调区间上增函数的图象从左向右是上升的,减函数的图象从左向右是下降的。(1)如果函数y=f(x)在某个区间是增函数或减函数,就说函数y=f(x)在这一区间具有(严格的)单调性,这一区间叫函数y=f(x)的单调增(减)区间。其中单调增区间和单调减区间统称为单调区间写出常见函数的单调区间并指明是增区间还是减区间),0(),0,(,0a),0(),0,(,0a单减区间是时单减区间是时),(,0a),(,0a单减区间是时单增区间是时),a2b[],a2b,(,0a),a2b[],a2b,(,0a单减区间是单增区间是时单增区间是单减区间是时1、函数的单调区间是2、函数y=ax+b(a≠0)的单调区间是3、函数y=ax2+bx+c(a≠0)的单调区间是xay用定义证明函数单调性的步骤:(1)取值.即设是该区间内的任意两个值,且21xx、21xx(2)作差变形.即作差并通过因式分解,配方,)()(21xfxf有理化等方法,向有利于判断差的符号的方向变形.(3)定号.确定差的符号.)()(21xfxf(4)判断.根据函数单调性的定义判断单调性.