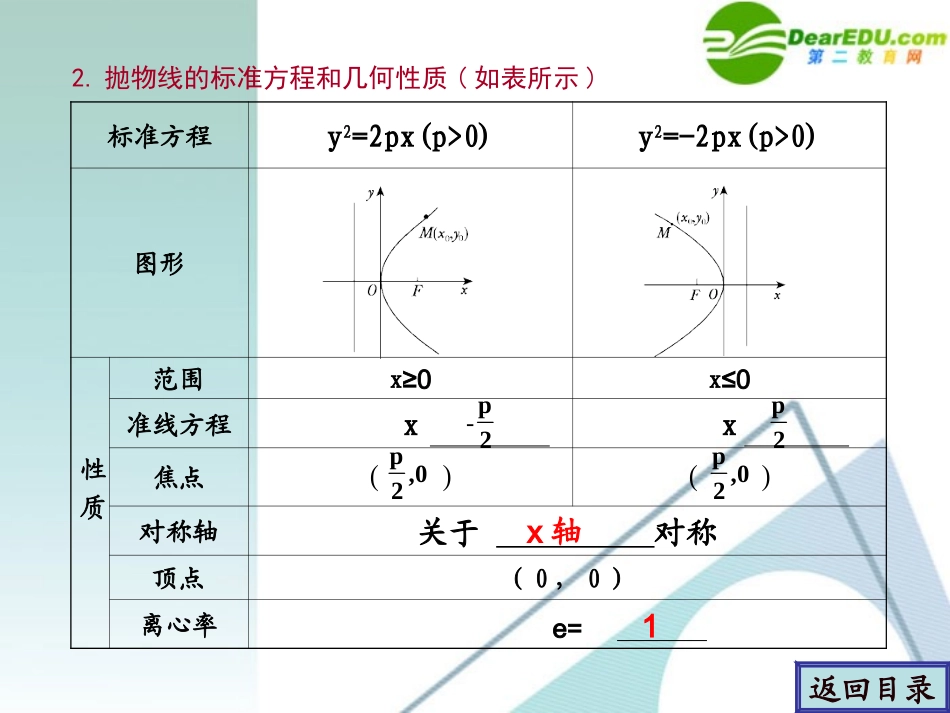
学案学案88抛物抛物线线返回目录1.抛物线的定义平面内与一个定点F和一条定直线l(l不经过点F)距离点的轨迹叫做抛物线.点F叫做抛物线的,直线l叫做抛物线的.相等焦点准线返回目录2.抛物线的标准方程和几何性质(如表所示)标准方程y2=2px(p>0)y2=-2px(p>0)图形性质范围x≥0x≤0准线方程xx焦点()()对称轴关于对称顶点(0,0)离心率e=p,02p,02-p2p2x轴11返回目录标准方程x2=2py(p>0)x2=-2py(p>0)图形性质范围y≥0y≤0准线方程xx焦点()()对称轴关于对称顶点(0,0)离心率e=p0,2p2-p0,2y轴-p2返回目录已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求出取最小值时P点的坐标.【分析】【分析】由定义知,抛物线上点P到焦点F的距离等于P到准线l的距离d,求|PA|+|PF|的问题可转化为|PA|+d的问题.考点一抛物线的定义考点一抛物线的定义返回目录【解析】【解析】将x=3代入抛物线方程y2=2x,得y=±. >2,A∴在抛物线内部.如图,设抛物线上点P到准线l:x=-的距离为d,由定义知|PA|+|PF|=|PA|+d,当PAl⊥时,|PA|+d最小,最小值为,即|PA|+|PF|的最小值为,此时P点纵坐标为2,代入y2=2x,得x=2,∴点P坐标为(2,2).66127272【评析】【评析】重视定义在解题中的应用,灵活地进行抛物线上的点到焦点的距离到准线距离的等价转化,是解决抛物线焦点弦有关问题的重要途径.返回目录*对应演练**对应演练*已知点P在抛物线y2=4x上,那么当点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为()A.(,-1)B.(,1)C.(1,2)D.(1,-2)A((1)点P到焦点距离等于点P到准线距离,即求点P到点Q与点P到准线距离之和最小时P点坐标,当QP垂直准线时,所求距离之和最小,P∴点纵坐标y0=-1,x∴0=,∴P(,-1).故应选A.)1414返回目录1414返回目录试分别求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:(1)过点(-3,2);(2)焦点在直线x-2y-4=0上.考点二求抛物线方程考点二求抛物线方程【分析】【分析】按先定位,再定量的原则求抛物线方程.【解析】【解析】(1)设所求的抛物线为y2=-2px(p>0)或x2=2py(p>0), 过点(-3,2),4=-2p(-3)∴或9=2p·2,∴p=或p=.所求的抛物线方程为y2=-x或x2=y,前者的准线方程是x=,后者的准线方程是y=-.返回目录239443981392返回目录(2)令x=0得y=-2,令y=0得x=4,即抛物线的焦点为(4,0)或(0,-2).当焦点为(4,0)时,=4,p=8.∴此时抛物线方程为y2=16x.当焦点为(0,-2)时,=2,∴p=4,此时抛物线方程为x2=-8y.故所求的抛物线方程为y2=16x或x2=-8y,对应的准线方程分别是x=-4或y=2.p2p2返回目录【评析】【评析】求抛物线方程的基本方法仍然是待定系数法,需要注意的是:(1)当坐标系已建立时,应根据条件确定抛物线方程属于四种类型的哪一种;(2)要注意把握抛物线的顶点、对称轴、开口方向与方程之间的对应关系;(3)要注意焦参数p的几何意义,并利用它的几何意义来解决问题,特别是当顶点不在原点时,更要注意利用参数p的几何意义,以及焦点到顶点的距离和顶点到准线的距离均为来求其方程.这里易犯的错误就是缺少对开口方向的讨论,设定一种形式的标准方程后求解,以致失去一解.反过来,也要注意由抛物线方程读有关信息,如参数p及顶点坐标,进而求出有关几何性质.p2返回目录*对应演练**对应演练*根据下列条件求抛物线的标准方程:(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;(2)过点P(2,-4);(3)抛物线焦点F在x轴上,直线y=-3与抛物线交于点A,|AF|=5.返回目录(1)双曲线方程化为,左顶点为(-3,0),由题意设抛物线方程为y2=-2px(p>0)且-=-3,p=6,∴∴方程为y2=-12x.(2)由于P(2,-4)在第四象限且对称轴为坐标轴,可设方程为y2=mx或x2=ny,代入P点坐标求得m=8,n=-1,∴所求抛物线方程为y2=8x或x2=-y.(3)设所求焦点在x轴上的抛物线方程为y2=2px(p≠0),A(m,-3),由抛物线定义得5=|AF|=|m+|,又(-3)2=2pm,p=±1∴或p=±9.故所求抛物线方程为y2=±2x或y2=±18x.22xy-=1916p2p2已知抛物线顶点在原点,焦点在坐标轴上,又知此抛物线上的一点A(m,-3)到焦点F的距离为5,求m的值,并写出此抛物线的方程.【分析】【分析】因点A(m,-3)在直线y=-3...