高中数学参数方程课件新人教B版选修4-4 课件VIP免费

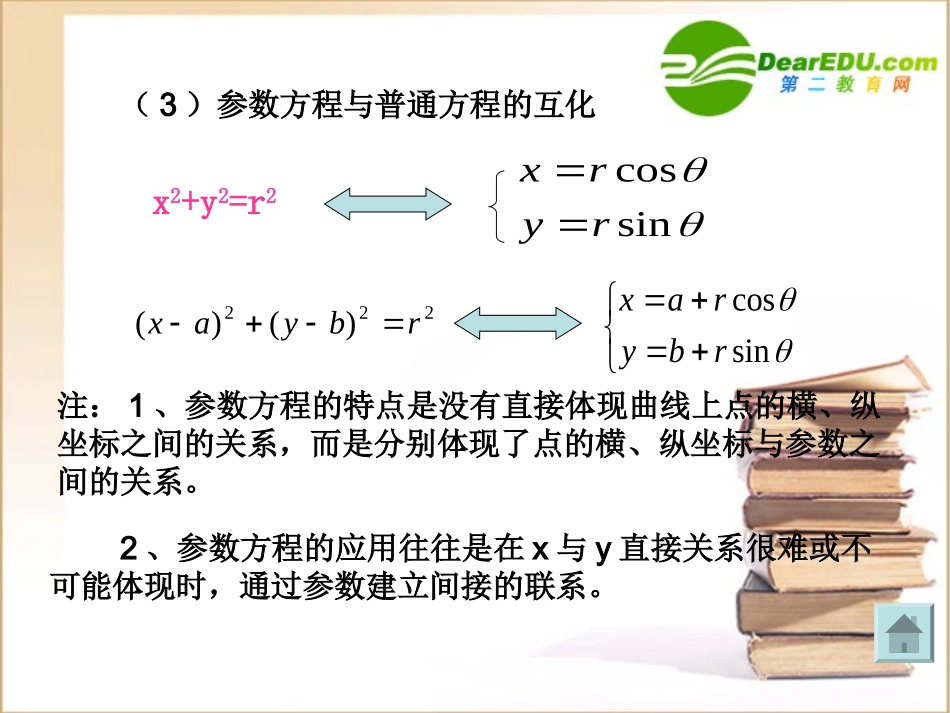
第二讲参数方程1、参数方程的概念（1）在取定的坐标系中，如果曲线上任意一点的坐标x、y都是某个变数t的函数，即并且对于t的每一个允许值，由上述方程组所确定的点M（x,y）都在这条曲线上，那么上述方程组就叫做这条曲线的参数方程，联系x、y之间关系的变数叫做参变数，简称参数。参数方程的参数可以是有物理、几何意义的变数，也可以是没有明显意义的变数。)()(tgytfx（2）相对于参数方程来说，前面学过的直接给出曲线上点的坐标关系的方程，叫做曲线的普通方程。（3）参数方程与普通方程的互化sincosryrxx2+y2=r2222)()(rbyaxsincosrbyrax注：1、参数方程的特点是没有直接体现曲线上点的横、纵坐标之间的关系，而是分别体现了点的横、纵坐标与参数之间的关系。2、参数方程的应用往往是在x与y直接关系很难或不可能体现时，通过参数建立间接的联系。sincosrbyrax1.圆的参数方程（1）轨迹问题（2）求最值4.应用5.小结2.参数方程与普通方程的概念3.参数方程与普通方程的互化（1）圆心在原点的圆参数方程（2）圆心不在原点的圆的参数方程观察1即的函数都是纵坐标、的横坐标点根据三角函数定义圆半径为的坐标为如果点,,,,),,(0yxPOPPryxPsincosryrx①并且对于的每一个允许值,由方程组①所确定的点P(x,y),都在圆O上.o思考1：圆心为原点，半径为r的圆的参数方程是什么呢？-555-5rp0P(x,y)我们把方程组①叫做圆心在原点、半径为r的圆的参数方程，是参数.sincos11ryrx?,)()(),(:22221那么参数方程是什么呢为的圆的标准方程、半径为圆心为思考rbyaxrbaO观察25-5-55v(a,b)oP(x,y)O1),(111yxP(a,b)r11111(,),(,)(,),,OabrOrOPxyOPxy圆心为、半径为的圆可以看作由圆心为原点、半径为的圆平移得到设圆上任意一点是圆上的点平移得到的由平移公式有又所以sincosrbyraxbyyaxx11例1、已知圆方程x2+y2+2x-6y+9=0，将它化为参数方程。解：x2+y2+2x-6y+9=0化为标准方程，（x+1）2+（y-3）2=1，∴参数方程为sin3cos1yx(θ为参数)练习：1.填空：已知圆O的参数方程是sin5cos5yx(0≤＜2)⑴如果圆上点P所对应的参数，则点P的坐标是355532,,22QQ如果圆上点所对应的坐标是则点对应的参数等于235,25322cos2.()2sin.,2.,2..xyABCD选择题：参数方程为参数表示的曲线是圆心在原点半径为的圆圆心不在原点但半径为的圆不是圆以上都有可能A半径为表示圆心为参数方程、填空题sin2cos2)1(:3yx的圆，化为标准方程为化为参数方程为把圆方程0142)2(22yxyx（2，-2）112222yxsin22cos21yx例3例2.如图,已知点P是圆x2+y2=16上的一个动点,点A是x轴上的定点,坐标为(12,0).当点P在圆上运动时,线段PA中点M的轨迹是什么?xMPAyO解:设M的坐标为(x,y),∴可设点P坐标为(4cosθ,4sinθ)∴点M的轨迹是以(6,0)为圆心、2为半径的圆。由中点公式得:点M的轨迹方程为x=6+2cosθy=2sinθx=4cosθy=4sinθ圆x2+y2=16的参数方程为例2.如图,已知点P是圆x2+y2=16上的一个动点,点A是x轴上的定点,坐标为(12,0).当点P在圆上运动时,线段PA中点M的轨迹是什么?解:设M的坐标为(x,y),∴点M的轨迹是以(6,0)为圆心、2为半径的圆。由中点坐标公式得:点P的坐标为(2x-12,2y)∴(2x-12)2+(2y)2=16即M的轨迹方程为(x-6)2+y2=4 点P在圆x2+y2=16上xMPAyO例2.如图,已知点P是圆x2+y2=16上的一个动点,点A是x轴上的定点,坐标为(12,0).当点P在圆上运动时,线段PA中点M的轨迹是什么?例3、已知点P（x，y）是圆x2+y2-6x-4y+12=0上动点，求（1）x2+y2的最值，（2）x+y的最值，（3）P到直线x+y-1=0的距离d的最值。解：圆x2+y2-6x-4y+12=0即（x-3）2+（y-2）2=1，用参数方程表示为sin2cos3yx由于点P在圆上，所以可设P（3+cosθ，2+sinθ），（1）x2+y2=(3+cosθ)2+(2+sinθ)2=14+4sinθ+6cosθ=14+2sin(θ+ψ).13(其中ta...