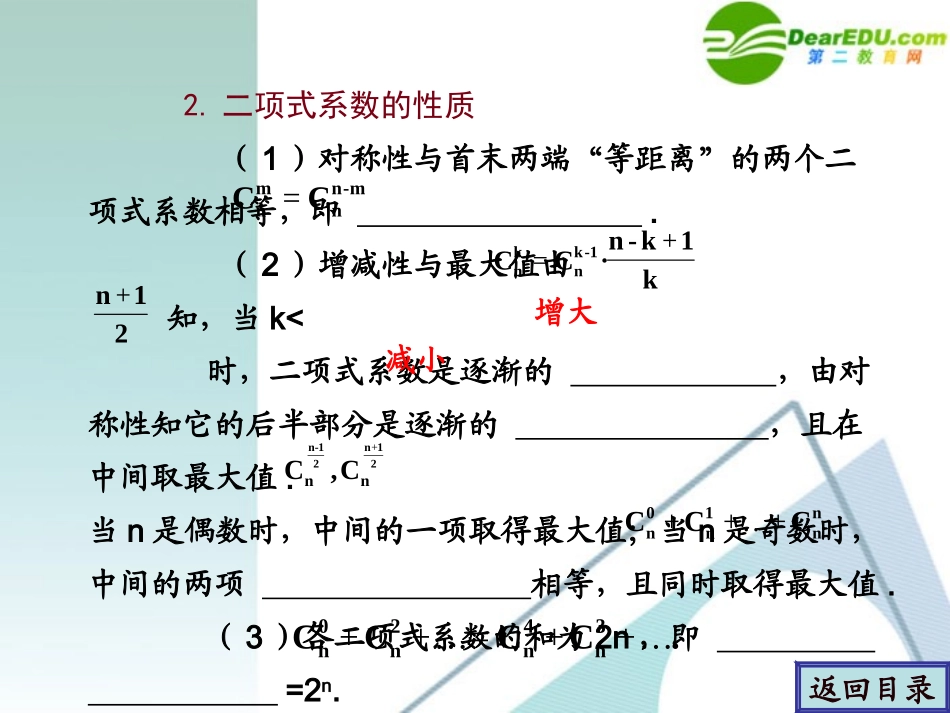
学案学案33二项式定理二项式定理返回目录1.二项式定理的内容(a+b)n=.右边的多项式叫做(a+b)n的,其中的系数(r=0,1,…,n)叫做展开式的,式中的第r+1项an-rbr叫做二项展开式的,记作Tr+1=(其中0≤r≤n,rN,∈nN*).∈rnCrnCN*)(nbCbaCbaCaCnnnkk-nkn1-1n1nn0n∈+…++…++二项展开式二项式系数通项rr-nrnbaC2.二项式系数的性质(1)对称性与首末两端“等距离”的两个二项式系数相等,即.(2)增减性与最大值由知,当k<时,二项式系数是逐渐的,由对称性知它的后半部分是逐渐的,且在中间取最大值.当n是偶数时,中间的一项取得最大值;当n是奇数时,中间的两项相等,且同时取得最大值.(3)各二项式系数的和为2n,即=2n.(4)奇数项的二项式系数的和等于偶数项的二项式系数的和,即返回目录k1k-n·CC-1knkn+=21n+.CCCC3n4n2n0n…++=…++m-nnmnCC=增大减小C,C21n21-nnn+nn1n0nCCC+…++(1)的展开式中x5的系数为.(2)若在(1+ax)5的展开式中x3的系数为-80,则a=.返回目录考点一求二次展开式的特定项考点一求二次展开式的特定项【分析】【分析】由通项公式列方程可得.8)x1-(x【解析】【解析】(1)二项展开式的通项为令8-=5,则r=2,∴T3=(-1)2··x5=28x5,∴x5的系数为28.(2)在二项展开式中通项公式Tr+1=(ax)r=·ar·xr,令r=3,得x3的系数:·a3=-80,∴a3=-8,a=-2.∴返回目录23r-8r8rr21-r-8r81r·x·C(-1))·(-xxCT==+r2328Cr5Cr5C35C【评析】【评析】(1)二项展开式的通项公式反映出展开式在指数、项数、系数等方面的内在联系,因此能运用二项展开式的通项公式求特定项、特定项的系数或指数.(2)求指定项的系数主要通过二项式定理的通项公式列方程求得,考查计算能力.返回目录若(x+)n展开式的二项式系数之和为64,则展开式的常数项为()A.10B.20C.30D.120B(由展开式的二项式系数之和为64,得2n=64,得n=6,则展开式中的第r+1项Tr+1=x6-r(x-1)r=x6-2r,令6-2r=0,得r=3.则展开式中的常数项为T4==20.故应选B.)返回目录*对应演练**对应演练*x1r6Cr6C36CB(1+2x)n的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项.【分析】【分析】根据条件可求出n;再根据n的奇偶性,确定二项式系数最大的项;系数最大的项则由不等式组确定.返回目录考点二增减性与最值问题考点二增减性与最值问题【解析】【解析】T6=(2x)5,T7=(2x)6,依题意有·25=·26n=8.∴(1+2x)8的展开式中二项式系数最大的项为T5=(2x)4=1120x4,设第r+1项系数最大,则有·2r≥·2r-1·2r≥·2r+1返回目录6nC5nC5nC6nC⇒48Cr8Cr8C-1r8C1r8C+1)-r-(81)!(r8!·2r)!-(8r!8!1)!r-(81)!-(r8!r)-(8r!8!·2++≥≥{{⇒2(8-r+1)≥rr≤6r+1≥2(8-r)r≥5又 rN∈,∴r=5或r=6,∴系数最大的项为T6=1792x5,T7=1792x6.返回目录{{⇒⇒5≤r≤6.【评析】【评析】①求二项式系数最大的项,要根据二项式系数的性质,n为奇数时中间两项的二项式系数最大,n为偶数时中间一项的二项式系数最大.②求展开式中系数最大项与求二项式系数最大项是不同的,需根据各项系数的正、负变化情况,一般采用列不等式组、解不等式组的方法.返回目录在(3x-2y)20的展开式中,求:(1)二项式系数最大的项;(2)系数绝对值最大的项;(3)系数最大的项.返回目录*对应演练**对应演练*(1)二项式系数最大的项是第11项,T11=310(-2)10x10y10=610x10y10.(2)设系数绝对值最大的项是第r+1项,·320-r·2r≥·319-r·2r+1·320-r·2r≥·321-r·2r-1,3(r+1)≥2(20-r)2(21-r)≥3r,解得≤r≤.所以r=8.即T9=312·28·x12y8是系数绝对值最大的项.返回目录1020C1020Cr20Cr20C1r20C+1r20C+于是{化简得{527528820C(3)由于系数为正的项为奇数项,故可设第2r-1项系数最大,于是·322-2r·22r-2≥·324-2r·22r-4·322-2r·22r-2≥·320-2r·22r,10r2+143r-1077≤010r2+163r-924≥0.解之得r=5,即2×5-1=9项系数最大.T9=·312·28·x12y8.返回目录2-2r20C2-2rC4-2r20C2r20C820C化简得{{设(2-x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值:(1)a0;(2)a1+a2+…+a100;(3)a1+a3+a5+…+a99;(4)(a0+a2+…+a100)2-(a1+a3+…+a99)2.返回目录考点三利用赋值法求二项...