高考数学复习(空间向量的线性运算) 试题VIP免费

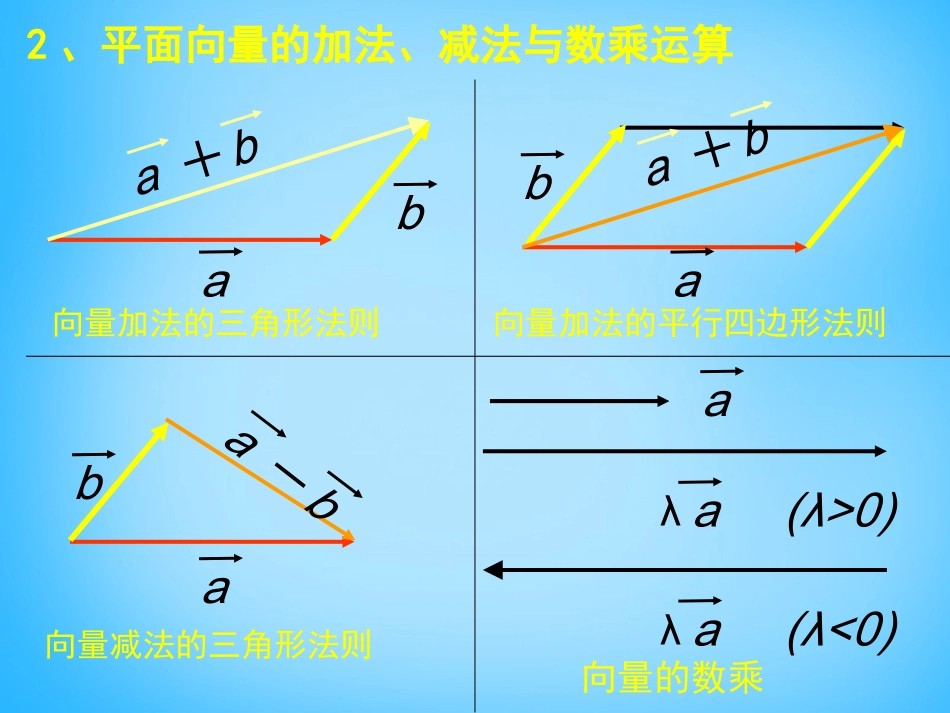
一、平面向量复习⒈定义：既有大小又有方向的量叫向量．几何表示法：用有向线段表示；相等的向量：长度相等且方向相同的向量．ABCD坐标表示法：2121,,,axyABxxyy��CDCDCD字母表示法：用字母a、b等或者用有向线段的起点与终点字母表示．AB�2、平面向量的加法、减法与数乘运算向量加法的三角形法则ab向量加法的平行四边形法则ba向量减法的三角形法则aba－ba＋ba(λ>0)λa(λ<0)λ向量的数乘aa＋b3、平面向量的加法与数乘运算律abbaaab()()abcabc()abab＋aa加法交换律：加法结合律：数乘分配律：数乘结合律：000a特别地推广:向量求和的多边形法则（1）首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点的向量；12233411nnnAAAAAAAAAA�（2）首尾相接的若干向量若构成一个封闭图形，则它们的和为零向量。12233410nAAAAAAAA�（3）△ABC中，D为BC中点，则�1AD=AB+AC2ADCB二、空间向量及其线性运算⒈空间向量：⑴定义：空间中具有大小和方向的量叫做向量．例如:空间中点的一个位移就是一个向量.⑵表示方法：,,abc①字母表示:②几何表示:有向线段AB�212121,,,,,axyzABxxyyzz��③坐标表示:a注意：两个向量的模可以比较大小（模为非负实数），但两个向量不可以比较大小。⑷向量的基线：表示空间向量的有向线段所在的直线叫做向量的基线。注意：基线是直线，不是线段，每一个向量都对应一条基线，而不同的向量可以有相同的基线。⑶向量的模(长度):表示向量的有向线段的长度叫向量的模,又叫向量的长度。记作aaAB��⑸几个常见的特殊向量：①相等向量：空间中同向且等长的有向线段表示同一向量或相等的向量，即大小、方向相同的两个向量；说明：1、向量不仅可以在平面上平移，还可以在空间中平移，一个向量在平移后和平移前的两个向量是相等向量，但这两个向量的基线不同。2、空间任意两个向量都可以平移到同一平面内，用这个平面内的两条有向线段表示。②零向量：起点与终点重合的向量叫零向量。记作：。零向量的模长为0，零向量的方向是任意的。000aa④相反向量：模长相等，方向相反的两个向量叫相反向量。,aaaa��③单位向量：模长为1的向量叫单位向量。1aa是单位向量⑤平行向量（共线向量）：如果空间中的一些向量的基线互相平行或重合，则这些向量叫平行向量或共线向量。记作：//ab规定：零向量与任意向量平行（共线）说明：平行（共线）向量的基线平行或重合，不同向量的基线可能相同。平行向量就是共线向量。ab思考:空间向量的运算系统?空间中任意两个向量的和、差、数乘运算法则和运算律??类比推理和化归的数学思想。平面空间⒉空间向量的线性运算：⑴空间向量的加法：abOCOAOB�baabACbBO说明：①空间中的任意两个向量的加法运算，都可以转化为共面向量，利用平行四边形法则和三内角形法则解决。②由于O点的选取是任意的，所以空间向量的加法运算与O点的位置选取无关。减法是加法的逆运算⑵空间向量的减法：⒉空间向量的线性运算：ABOBOAba�aAbBO-aB（后-前，指向被减向量）⑶空间向量的数乘运算：aa0aPO0aP当时，与共线同向。0aa当时，与共线反向。a0a当时，00a⒊空间向量加法与数乘向量运算律：abba()()abcabc(),()ababaaa⑵加法结合律：⑶数乘分配律：bca+b+cabca+b+ca+bb+c⑴加法交换律：a()()aa(4)数乘结合律：有限个向量求和，交换相加向量的顺序其和不变。对空间向量的加法、减法与数乘向量的说明空间向量的运算就是平面向量运算的推广。要会类比平面向量的有关结论对空间向量作出推广。4.四个重要结论:⑴空间向量加法的多边形法则：空间中首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点...