高一数学函数的单调性(一)课件VIP免费

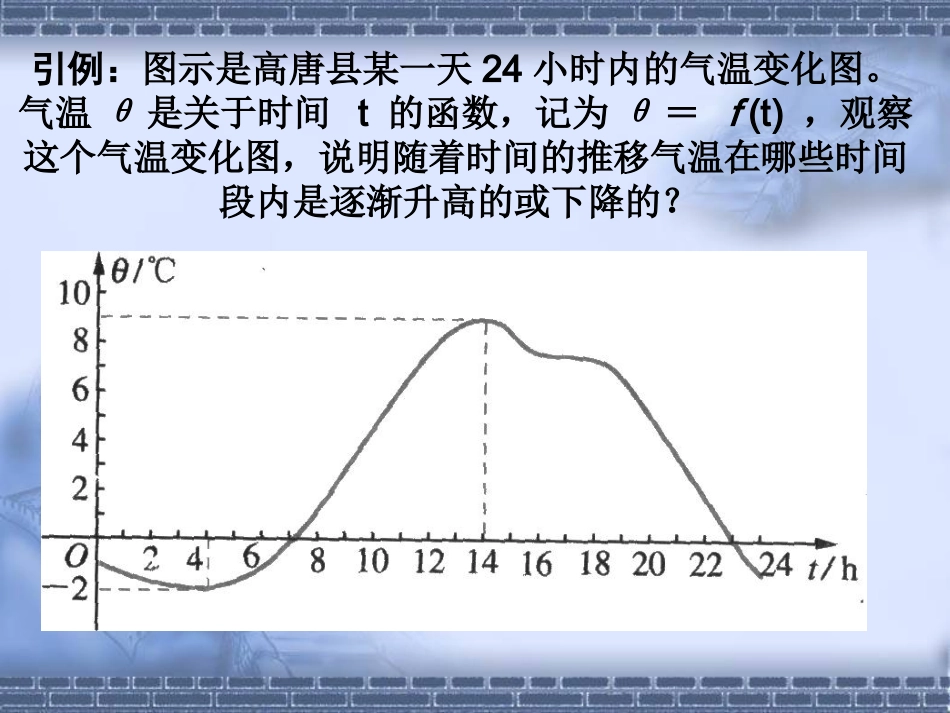
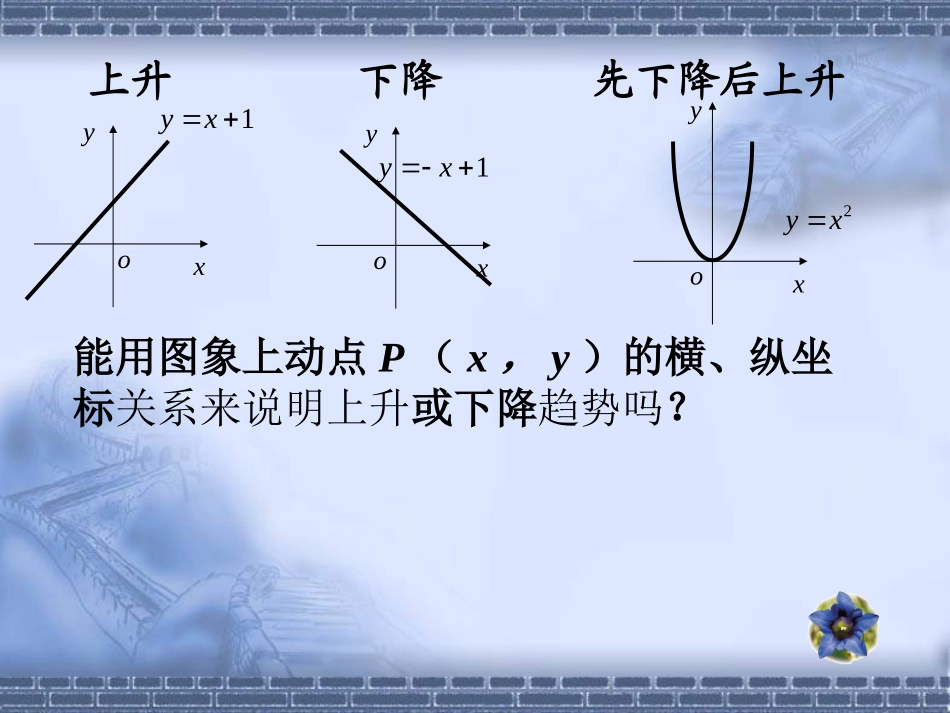
高唐二中王金印引例：图示是高唐县某一天24小时内的气温变化图。气温θ是关于时间t的函数，记为θ＝f(t)，观察这个气温变化图，说明随着时间的推移气温在哪些时间段内是逐渐升高的或下降的？能用图象上动点P（x，y）的横、纵坐标关系来说明上升或下降趋势吗？xyo1yxxyo1yxxyo2yx先下降后上升下降上升在某一区间内，当x的值增大时,函数值y反而减小——图像在该区间内逐渐下降。x…-4-3-2-101234…f(x)=x2……16941014916xyo2yx当x的值增大时,函数值y也增大——图像在该区间内逐渐上升；思考:函数在区间上随着x的增大函数值也增大,那么在区间上任意两个不同的,试问与有什么关系?2()fxx0,0,12,xx1()fx2()fx0xy1x2x2fx12xx21x22x<2fxx12xx12fxfx在区间上是增函数0,1fxOxyx1x2f(x1)f(x2)设函数y=f(x)的定义域为I,区间DI.如果对于属于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1f(1)，则函数f(x)在R上是增函数；（3）x1,x2取值的任意性yxO12f(1)f(2)那么就说在f(x)这个区间上是单调增函数，D称为f(x)的单调增区间.那么就说在f(x)这个区间上是单调减函数，D称为f(x)的单调减区间.Oxyx1x2f(x1)f(x2)类比单调增函数的研究方法定义单调减函数.xOyx1x2f(x1)f(x2)设函数y=f(x)的定义域为I,区间DI.如果对于属于定义域I内某个区间D上的任意两个自变量的值x1,x2，设函数y=f(x)的定义域为I,区间DI.如果对于属于定义域I内某个区间D上的任意两个自变量的值x1,x2，当x1单调区间例1下图是定义在[－5，5]上的函数y＝f（x）的图象，根据图象说出y＝f（x）的单调区间，以及在每一单调区间上，y＝f（x）是增函数还是减函数.[1，3），[3，5].解：y＝f（x）的单调区间有[－5，－2），[－2，1）其中y＝f（x）在[－5，－2），[1，3）上是减函数，在[－2，1），[3，5）上是增函数.1xy-1-23-5O12345-2-3-42-1例2.物理学中的玻意耳定律(k为正常数)告诉我们,对于一定量的气体,当其体积减小时,压强p将增大,试用函数的单调性证明之.kpV则1212()()kkpVpVVV2112VVkVV12,0,VV，且12VV21120,0VVVV1212()()0,()()pVpVpVpV所以函数在区间上是减函数.,0,kpVV0,证明：设是定义域上任取两个实数,且0,12VV12,VV又0k,于是取值作差变形定号结论证明函数单调性的一般步骤:取值作差变形定号结论证明函数在上是减函数.21fxx,证明小结1.函数单调性的定义中有哪些关键点？2.判断函数单调性有哪些常用方法？3.你学会了哪些数学思想方法？作业2、证明函数f（x）=-x2在上是减函数。,01、教材p39/1,2,3证明：在区间上任取两个值且,12,xx12xx则1212()()21(21)fxfxxx122121xx212()xx12xx12,,xx，且210xx1212()()0,()()fxfxfxfx所以函数在区间上是减函数.21yx,返回练习1:图示是高唐县某一天24小时内的气温变化图。气温θ是关于时间t的函数，记为θ＝f(t)，根据图象说出θ＝f(t)的单调区间，以及在每一单调区间上，θ＝f(t)是增函数还是减函数.