高二数学上册 8.2(向量的数量积)课件1 沪教版 课件VIP免费

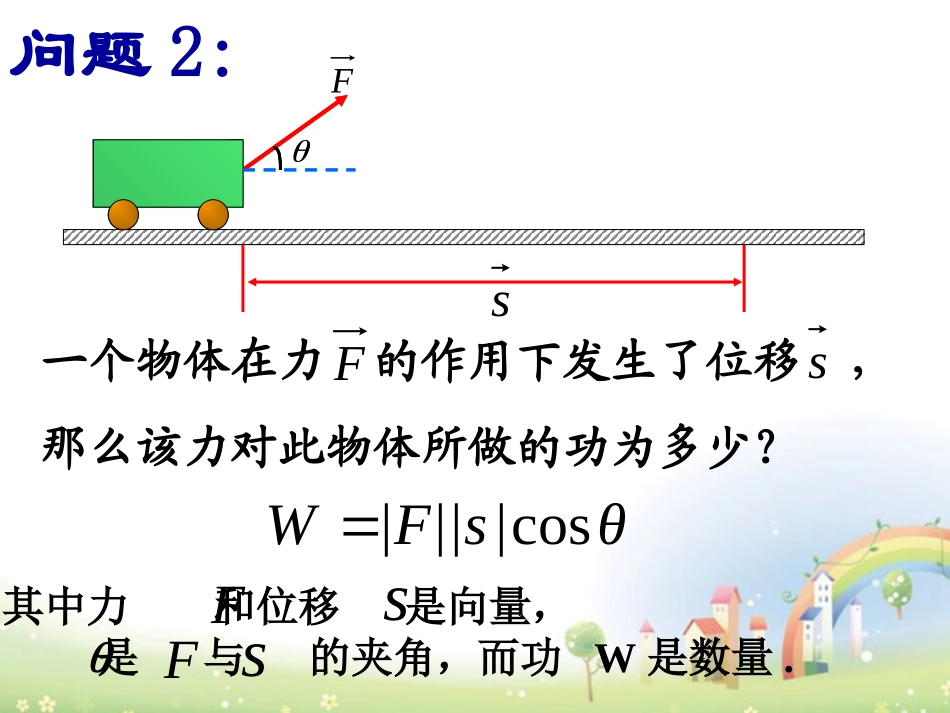
问题1:我们学习了向量的哪些运算？这些运算的结果是什么？平面向量的加法、减法和数乘三种运算；运算的结果仍是向量问题2:Fs一个物体在力的作用下发生了位移，那么该力对此物体所做的功为多少？Fsθ|s||F|Wcos其中力和位移是向量，是与的夹角，而功W是数量.FssF将公式中的力与位移推广到一般向量θ|s||F|Wcos功是力与位移的大小及其夹角余弦的乘积；结果是两个向量的模及其夹角余弦的乘积。出现了向量的一种新的运算.0,的夹角，其中与向量叫做向量的夹角、那么射线，作为起点，，如果以、对于两个非零向量baOBOAbOBaOAObaOABab1、向量的夹角方向相同；与，则向量）若（ba01OABbaOABba方向相反；与，则向量）若（ba2OABabbaba23记作垂直，与，则向量）若（互相平行。与时，向量或即当ba0规定：零向量与其它向量的夹角可根据需要确定。如图,等边三角形ABC中,求求（1）AB与AC的夹角；（2）AB与BC的夹角。ABC平移向量至始点重合12060'CD0120OABba2、向量的数量积的定义ba、），（0θ|b||a|cosba与ba一般地，如果两个非零向量的夹角为那么我们把叫做向量的数量积，记作，即θcos|b||a|baθcos|b||a|ba2、向量的数量积是一个数量,不是向量。向量的数量积的说明3、规定00a1、不能写成且不能省略。ba，ba”“当为非零向量时，数量积的正负由夹角余弦值决定。b,a2aaa4、特别记.//(3)(2)120)1(,4||,5||10bababababababa时，求当；时，求当；时，求的夹角是与当已知、例如图所示，等边三角形ABC的边长为1，求（1）的数量积；（2）的数量积；ABCBCAB与ACAB与ba,ba同向时与）当（1||||baba,ba反向时与当||||bababa(2)3、向量的数量积的重要性质θbab,a的夹角为与均为非零向量，且已知即|b||a|bab//a0两个重要的充要条件aa(5)3、向量的数量积的重要性质θcos(4)abab|b||a||ba|）（3?|b||a||ba|成立吗20acosaa22aa即_______254912|(1)θba,ba|b||a的夹角与则，，若三角形。为时，当，已知_______ABC0ABABC(2)ba,bAC,a_______|8(3)2|aaa，则满足已知向量1350直角22例2、填空00)1(a(×)(×)00)2(abababa//|,|||)3(则若(√)22||)4(aaaa(√).0,0)5(中至少有一个为与则若baba(×)1、已知均为非零向量,试判断下列说法是否正确？cba,,奎屯王新敞新疆的形状是，则中，、在ABCBCABABC03（）的形状是，则中，、在ABCBCABABC02A、锐角三角形C、钝角三角形D、不能确定B、直角三角形（）DCABC问题:（1）实数乘法有哪些运算律？（2）这些运算律是否能适用于向量的数量积的运算？4、向量的数量积的运算律实数乘法baab）交换律：（1)()(2bcacab）结合律：（bcaccba)(3）分配律：（向量的数量积类比猜想abba）交换律：（1)()(2cbacba）结合律：（cbcacba)(3）分配律：（)()()(4bababa）数乘结合律：（是否都成立？验证向量数量积的运算律ababbabacoscosabba）交换律：（1都成立？能否对任意向量c,b,a)cb(ac)ba(思考：即：向量数量积运算不满足结合律若0,若0，)()()(2bababa）数乘结合律：（0，若则显然成立的夹角分别是什么？与；与；与)b(abab)a(的夹角又是什么？与；与；与)b(abab)a(cbcacba)(3）分配律：（如何验证？或通过向量数量积的坐标表示验证。可借助向量数量积的几何意义验证；5、向量的数量积的几何意义如图，作出││cosθ，并说出它的几何意义；││cosθ的几何意义又是什么？ba(B1)┐B1┐B1OBAθ(1)baBOA┓θ（3）abaBAOθ(2)b││cosθ叫做向量在向量上的投影，││cosθ叫做向量在向量上的投影.bbbaaa1cosbOB��1cosbOB��cos0b0222(B1)┐B1┐B1OBAθ(1)baBOA┓θ（3）abaBAOθ(2)b5、向量的数量积的几何意义(1)投影是一个数量，不是向...