高一数学三角函数小结与复习课件 人教版 课件VIP免费

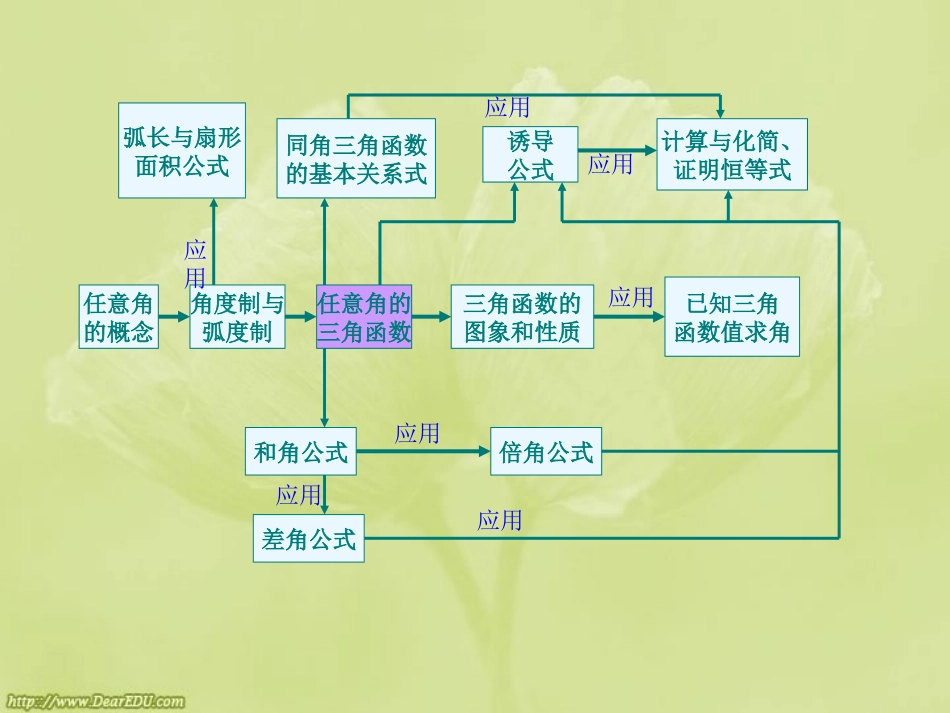
《三角函数》小结与复习《三角函数》小结与复习一、知识网络二、解题方法三、例题选讲四、小结与作业宏观思路微观直觉任意角的概念角度制与弧度制任意角的三角函数三角函数的图象和性质已知三角函数值求角弧长与扇形面积公式同角三角函数的基本关系式诱导公式计算与化简、证明恒等式和角公式差角公式倍角公式应用应用应用应用应用应用应用一、三角函数的定义sinα=ryrxxycosα=tanα=设P(x，y)是角α终边上的任意一点，=rOPOP（x，y）xy·二、同角三角函数的基本关系式商数关系：倒数关系：cos;sintancoscotsin222222;1tanssec;1cotcinos1sccsincscta1,cncots11,osec平方关系：三、诱导公式sincostan－α－sinαcosα－tanαπ－αsinα－cosα－tanαπ＋α－sinα－cosαtanα2π－α－sinαcosα－tanα2kπ＋αsinαcosαtanα函数角函数名不变,符号看象限π/2±α,3π/2±α的三角函数值等于α的余角的三角函数值，前面加上把α看成锐角时原函数的符号.(函数名改变,符号看象限)四、和（差）角公式sincoscossin)sin(sinsincoscos)cos(tantan1tantan)tan(五、倍角公式cossin22sin2222sin211cos2sincos2cos2tan1tan22tan它们的内在联系及推导线索如下：S(α＋β)C(α＋β)S(α－β)C(α－β)S2αC2αT(α－β)T(α＋β)T2α六、正弦、余弦、正切函数的图象和性质函数正弦函数余弦函数正切函数图象定义域RR值域[－1，1][－1，1]R周期性最小正周期2π最小正周期2π最小正周期π奇偶性奇函数偶函数奇函数单调性Zkkxx,2七、三角函数的应用三角函数的应用主要是运用三角公式，进行简单三角函数式的化简、求值和恒等式的证明（包括引出积化和差、和差化积、半角公式，但不要求记忆）。在掌握本章的知识的同时，还应注意到本章中大量运用的化归思想，这是一种重要的数学思想。我们用过的化归包括以下几个方面：三角函数的应用1、把未知化归为已知。例如用诱导公式把求任意角的三角函数值逐步为求锐角三角函数值。2、把特殊化归为一般。例如把正弦函数的图象逐步化归为函数y=Asin(ωx+φ)，xR∈（其中A＞0，ω＞0）的简图，把已知三角函数值求角化归为求[0，2π]上适合条件的角的集合等。3、等价化归。例如进行三角函数式的化简、恒等变形和证明三角恒等式。八、已知三角函数值求角已知三角函数值求角x（仅限于[0，2π]）的解题步骤：1、如果函数值为正数，则求出对应的锐角x0；如果函数值为负数，则求出与其绝对值相对应的锐角x0；2、由函数值的符号决定角x可能的象限角；3、根据角x的可能的象限角得出[0，2π]内对应的角：如果x是第二象限角，那么可以表示为π－x0如果x是第三象限角，那么可以表示为π＋x0如果x是第四象限角，那么可以表示为2π－x0九、三角解题常规宏观思路分析差异寻找联系促进转化指角的、函数的、运算的差异利用有关公式，建立差异间关系活用公式，差异转化，矛盾统一微观直觉1、以变角为主线，注意配凑和转化；2、见切割，想化弦；个别情况弦化切；3、见和差，想化积；见乘积，化和差；4、见分式，想通分，使分母最简；5、见平方想降幂，见“1±cosα”想升幂；6、见sin2α，想拆成2sinαcosα；7、见sinα±cosα或9、见cosα·cosβ·cosθ····，先运用sinα+sinβ=pcosα+cosβ=q8、见asinα+bcosα，想化为的形式若不行，则化和差想两边平方或和差化积)sin(22basin22sincos应用专题－三角代换（1）切割化弦例1、已知试用k表示22sinsin2()1tan42ksincos应用专题－三角代换（2）“1”的代换tan1tan1xx例2、已知求的值2sinsincos2xxx（3）分拆与配凑例3、的值是＿＿tan20tan403tan20tan40例４、已知330,cos()4444535sin(),413求sin()的值应用专题－三角代换（４）升幂与降幂例５、求证：48sincos44cos23例6、求4444357sinsinsinsin1616...