高中数学 12(函数的概念和性质)精品课件 湘教版必修1 课件VIP免费

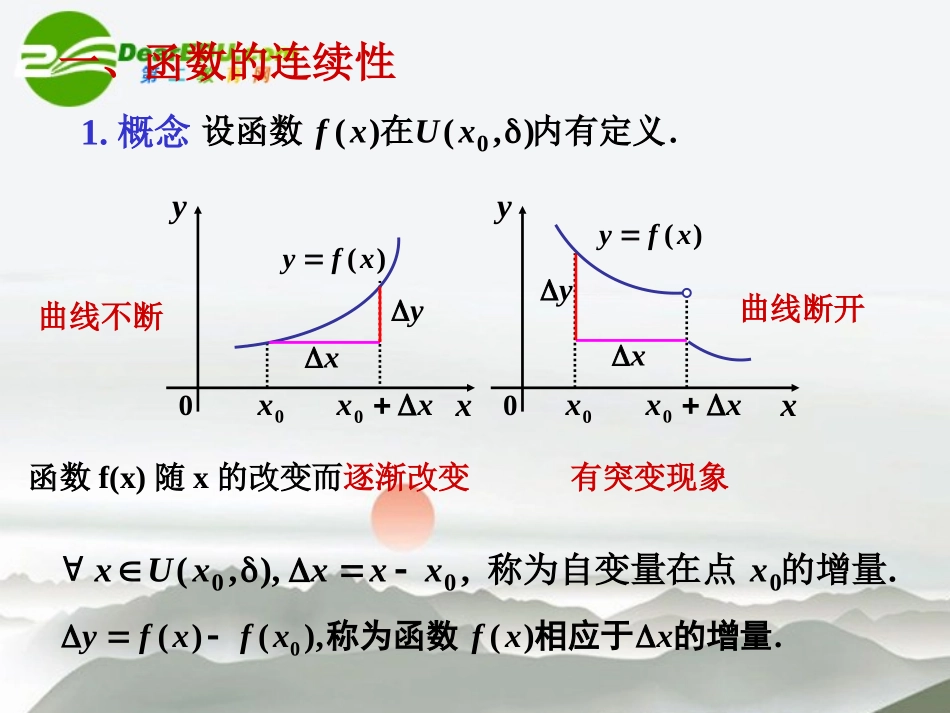
【数学】１．２《函数的概念和性质》精品课件（湘教版必修1）函数的概念与性质1、函数的连续性2、函数的间断点3、闭区间上连续函数的性质1.概念.,),,(000的增量称为自变量在点xxxxxUx.)(),()(0的增量相应于称为函数xxfxfxfy一、函数的连续性xy00xxx0)(xfyxyxy00xxx0xy)(xfy曲线不断曲线断开.),()(0内有定义在设函数xUxf函数f(x)随x的改变而逐渐改变有突变现象2.连续的定义P50定义1设函数)(xf在)(0xU内有定义,如果当自变量的增量x趋向于零时,对应的函数的增量y也趋向于零,即0lim0yx或0)]()([lim000xfxxfx,那末就称函数)(xf在点x0连续,x0称为)(xf的连续点.,0xxx设),()(0xfxfy,00xxx就是).()(00xfxfy就是注：1)函数f(x)在x0连续的等价写法(满足定义1的条件):.)()(lim000xfxxfx.)()(lim00xfxfxx2)若y=f(x)在x0处不连续，则称y=f(x)在x0处间断。.)()(,,0,0:00xfxfxx恒有时使当即3)极限与连续的关系:极限连续连续函数必有极限,有极限不一定是连续函数.例如.0/sin,1/sinlim0处不连续在但函数xxxxxx;)(lim0Axfxx.)()(lim00xfxfxx例1.0,0,0,0,1sin)(处连续在试证函数xxxxxxf证,01sinlim0xxx,0)0(f又.0)(处连续在函数xxf),0()(lim0fxfx3.单侧连续;)(),()0(,],()(0000处左连续在点则称且内有定义在若函数xxfxfxfxaxf定理.)()(00处既左连续又右连续在是函数处连续在函数xxfxxf.)(),()0(,),[)(0000处右连续在点则称且内有定义在若函数xxfxfxfbxxf例2.0,0,0,0,)(/1处的连续性在讨论函数xxxexfx解0lim)(lim/100xxxexf),0(f),0(f右连续但不左连续,.0)(处不连续在点故函数xxfxxxexf/100lim)(lim4.连续函数与连续区间在区间上每一点都连续的函数,叫做在该区间上的连续函数,或者说函数在该区间上连续..],[)(,,,),(上连续在闭区间函数则称处左连续在右端点处右连续并且在左端点内连续如果函数在开区间baxfbxaxba连续函数的图形是一条连续而不间断的曲线.例如,基本初等函数在其定义域上连续,初等函数在其定义区间上连续.例3.),(sin内连续在区间函数证明xy证),,(x任取xxxysin)sin()2cos(2sin2xxx,1)2cos(xx.2sin2xy则,0,时当对任意的,sin有,2sin2xxy故.0,0yx时当.),(sin都是连续的对任意函数即xxy例4.设0,sin0,)(2xxbxxbxaxfbxbxxsinlim0abxax)(lim20解：.ba在x=0处连续，求常数a与b应满足的关系。:)(0条件处连续必须满足的三个在点函数xxf;)()1(0处有定义在点xxf;)(lim)2(0存在xfxx).()(lim)3(00xfxfxx).()(),()(,00或间断点的不连续点为并称点或间断处不连续在点函数则称要有一个不满足如果上述三个条件中只xfxxxf二、函数的间断点1.跳跃间断点.)(),0()0(,,)(0000的跳跃间断点为函数则称点但存在右极限都处左在点如果xfxxfxfxxf例4.0,0,1,0,)(处的连续性在讨论函数xxxxxxf解,0)00(f,1)00(f),00()00(ff.0为函数的跳跃间断点xoxy2.可去间断点.)()(),()(lim,)(00000的可去间断点为函数义则称点处无定在点或但处的极限存在在点如果xfxxxfxfAxfxxfxx例5.1,1,11,10,1,2)(处的连续性在讨论函数xxxxxxxfoxy112xy1xy2解,1)1(f,2)01(f,2)01(f2)(lim1xfx),1(f.0为函数的可去间断点x如例5中,,2)1(f令.1,1,1,10,2)(处连续在则xxxxxxf跳跃间断点与可去间断点统称为第一类间断点.特点.0处的左、右极限都存在函数在点xoxy112注意可去间断点只要改变或者补充间断处函数的定义,则可使其变为连续点.3.第二类间断点.)(,)(00的第二类间断点为函数则称点在右极限至少有一个不存处的左、在点如果xfxxxf例6.0,0,,0,1)(处的连续性在讨论函数xxxxxxf解oxy,0)00(f,)0...