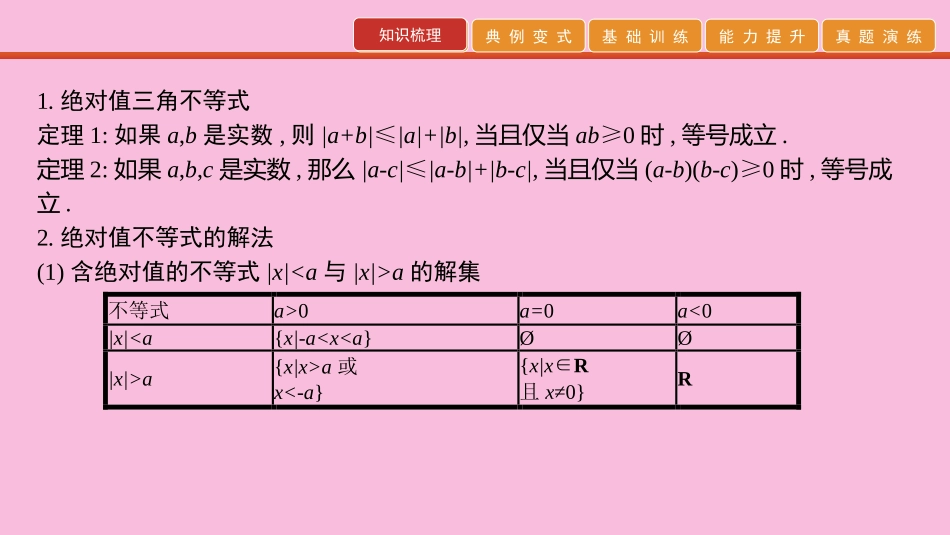
知识梳理典例变式基础训练能力提升真题演练第30讲不等式选讲知识梳理典例变式基础训练能力提升真题演练知识梳理1.绝对值三角不等式定理1:如果a,b是实数,则|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.定理2:如果a,b,c是实数,那么|a-c|≤|a-b|+|b-c|,当且仅当(a-b)(b-c)≥0时,等号成立.2.绝对值不等式的解法(1)含绝对值的不等式|x|
a的解集不等式a>0a=0a<0|x|a{x|x>a或x<-a}{x|x∈R且x≠0}R知识梳理典例变式基础训练能力提升真题演练知识梳理(2)|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法①|ax+b|≤c⇒-c≤ax+b≤c;②|ax+b|≥c⇒ax+b≥c或ax+b≤-c.(3)|x-a|+|x-b|≥c,|x-a|+|x-b|≤c(c>0)型不等式的解法:①利用绝对值不等式的几何意义求解;②利用零点分段法求解;③构造函数,利用函数的图象求解.知识梳理典例变式基础训练能力提升真题演练知识梳理3.基本不等式定理1:设a,b∈R,则a2+b2≥2ab,当且仅当a=b时,等号成立.定理2:如果a,b为正数,则𝑎+𝑏2≥ξ𝑎𝑏,当且仅当a=b时,等号成立.定理3:如果a,b,c为正数,则𝑎+𝑏+𝑐3≥3ξ𝑎𝑏𝑐,当且仅当a=b=c时,等号成立.定理4:(一般形式的算术—几何平均不等式)如果a1,a2,…,an为n个正数,则𝑎1+𝑎2+…+𝑎𝑛𝑛≥nඥ𝑎1𝑎2…𝑎𝑛,当且仅当a1=a2=…=an时,等号成立.知识梳理典例变式基础训练能力提升真题演练知识梳理4.不等式的证明方法证明不等式常用的方法有比较法、综合法、分析法、反证法、放缩法等.(1)比较法:①比差法的依据是:a-b>0⇔a>b,步骤是:“作差→变形→判断差的符号”.变形是手段,变形的目的是判断差的符号.②比商法:若B>0,欲证A≥B,只需证𝐴𝐵≥1.(2)综合法与分析法:①综合法:利用某些已经证明过的不等式和不等式的性质,推导出所要证明的不等式,这种方法叫综合法.即“由因导果”的方法.②分析法:从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题,如果能够肯定这些充分条件都已经具备,那么就可以判定原不等式成立,这种方法叫作分析法.即“执果索因”的方法.知识梳理典例变式基础训练能力提升真题演练典例变式题型一含绝对值不等式的解法【例1】设函数f(x)=|x-a|.(1)当a=2时,解不等式f(x)≥7-|x-1|;(2)若f(x)≤1的解集为[0,2],求a的值.【解析】(1)当a=2时,不等式为|x-2|+|x-1|≥7,所以ቄ𝑥<1,2-𝑥+1-𝑥≥7或ቄ1≤𝑥≤2,2-𝑥+𝑥-1≥7或൜𝑥>2,𝑥-2+𝑥-1≥7,所以不等式的解集为(-∞,-2]∪[5,+∞).(2)f(x)≤1即|x-a|≤1,解得a-1≤x≤a+1,而f(x)≤1的解集是[0,2],所以൜𝑎-1=0,𝑎+1=2,解得a=1.知识梳理典例变式基础训练能力提升真题演练典例变式【规律方法】|x-a|+|x-b|≥c(或≤c)型不等式的解法知识梳理典例变式基础训练能力提升真题演练典例变式变式训练一1.解不等式|x+3|-|2x-1|<𝑥2+1.解:(1)当x<-3时,原不等式化为-(x+3)-(1-2x)<𝑥2+1,解得x<10,所以x<-3.(2)当-3≤x<12时,原不等式化为(x+3)-(1-2x)<𝑥2+1,解得x<-25,所以-3≤x<-25.(3)当x≥12时,原不等式化为(x+3)-(2x-1)<𝑥2+1,解得x>2,所以x>2.综上可知,原不等式的解集为ቄ𝑥|𝑥<-25或𝑥>2ቅ知识梳理典例变式基础训练能力提升真题演练典例变式2.已知函数f(x)=|2x-a|+a.(1)当a=2时,求不等式f(x)≤6的解集;(2)设函数g(x)=|2x-1|.当x∈R时,f(x)+g(x)≥3,求a的取值范围.解:(1)当a=2时,f(x)=|2x-2|+2.解不等式|2x-2|+2≤6得-1≤x≤3.所以f(x)≤6的解集为{x|-1≤x≤3}.(2)当x∈R时,f(x)+g(x)=|2x-a|+a+|1-2x|≥|2x-a+1-2x|+a=|1-a|+a,所以当x∈R时,f(x)+g(x)≥3等价于|1-a|+a≥3.①当a≤1时,①等价于1-a+a≥3,无解.当a>1时,①等价于a-1+a≥3,解得a≥2.所以a的取值范围是[2,+∞).知识梳理典例变式基础训练能力提升真题演练典例变式题型二绝对值不等式性质的应用【例2】设不等式|x-2|