必修1-函数的奇偶性VIP免费

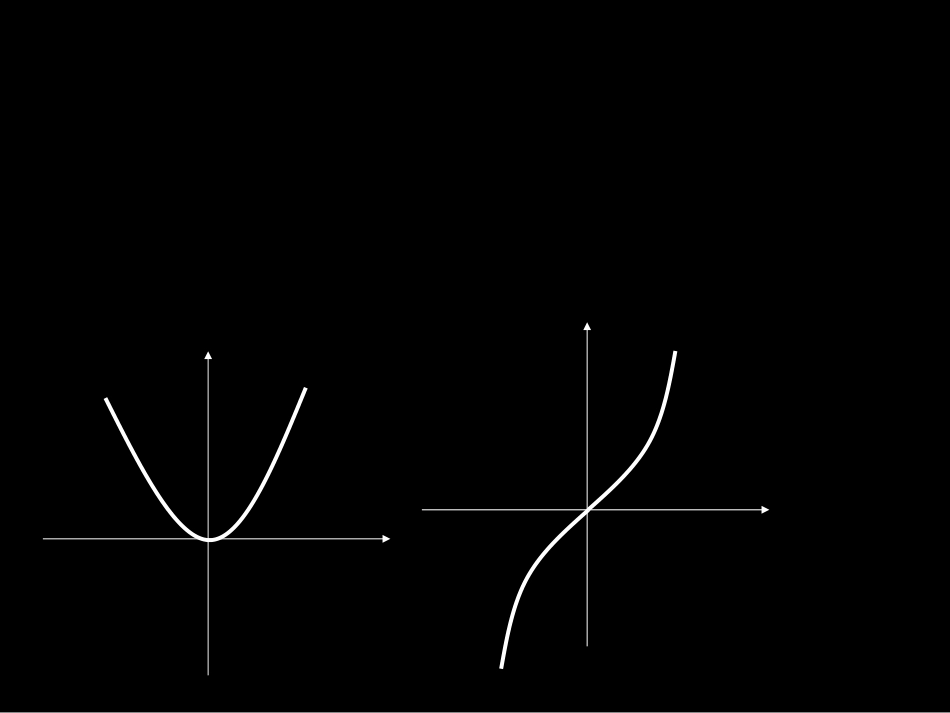
:.函数的奇偶性定义一.)(),()(,),(.1就叫做奇函数那么都有内任意一个如果对于定义域对于函数xfxfxfxIxf函数的奇偶性.)(),()(,),(.2就叫做偶函数那么都有内任意一个如果对于定义域对于函数xfxfxfxIxf:.价形式函数的奇偶性定义的等二1)()(0)()()()(xfxfxfxfxfxf:.2函数的奇偶性判断方法:).1利用定义;:).2看从左至右图象的走向利用图象;,对称看定义域是否关于原点①求定义域;)()(,的关系与则考察称②若定义域关于原点对xfxf:.3奇偶函数的图象特征;).1图象关于原点对称奇函数;).2轴对称图象关于偶函数yyxxOyxO2)(xxf3)(xxf:.4一些特殊函数的奇偶性0),(,)().1mmmxaxf;)(,0是偶函数时①当xfa;0)(,0既是奇函数又是偶函数时②当xfa11).4xxaay)1lg().62xxy)(21).2xxaay)(21).3xxaayxxya22log).5xxy22).7:.5论与函数奇偶性相关的结;0)0(,)().1fxf则在原点有定义奇函数;;;;:).2偶偶④偶偶偶③偶偶奇②奇奇奇①奇在公共定义域内;],[],[).3上有相同的单调性和奇函数在abba;],[],[).4上有相反的单调性和偶函数在abba;0)().623cadcxbxaxxf为偶函数函数;0)().723dbdcxbxaxxf为奇函数函数,),0().5单调递增若偶函数在||||)()(2121xxxfxf.)(),1()(,0,)(.1的解析式试求函数时且当上的奇函数为已知函数xfxxxfxRxf:解,0,0xx时设),1()(xxxf),1()(,0,)(xxxfxRxf时且当上的奇函数为函数0)0(),()(fxfxf)0(),1()(xxxxf)0(),1()(xxxxf。)0()1()0(0)0()1()(xxxxxxxxf.___________)3(,8)3(,5)()()(,)()(FFxngxmfxFRxgxf则且若上的奇函数都是定义在与已知函数)()(),()()()(xgxgxfxfRxgxf上的奇函数都是定义在与①函数5)3()3()3(ngmfF②5)3()3(ngmf85)3()3(ngmf3)3()3(ngmf5)3()3()3(ngmfF③253:分析.________)3()2(,1)2()3(,)()07.(2ffffxfy则若为奇函数已知函数辽宁.________)2()1(,3)2()1(3)1()2(,)()07.(3ffffffxfy则若为奇函数已知函数上海是偶函数是偶函数是奇函数是奇函数)()(.)()(.|)(|)(.)()(..4xfxfDxfxfCxfxfBxfxfAbDbCbBbAafbafxxxf1.1...)()(,)(,11lg)()07.(5则若已知函数辽宁32.32.32.32.)()(,23)(.6xyDyCxyBxyAxfyxyxfy的表达式为则图象关于原点对称的的图像与函数如果函数.____,121)(.8aaxfx则为奇函数已知函数.________,))(1()()07.(7aaxxxf则为偶函数设函数宁夏.)8()1)(8()(.92的奇偶性判断函数xxxxxf._____,3;1|;|;1:.102其中是偶函数的是④③②①已知下列函数xyxxyxyxy}25023|{.}250023|{.}023|{.}250|{.)(21)(,2)(,0,)(.11xxxDxxxCxxBxxAxfxxfxRxfy或或的解集是那么不等式时当上的奇函数是定义在已知函数020002)(:xxxxxxf解析Oxy2222}25023|{.}250023|{.}023|{.}250|{.)(21)(,2)(,0,)(.11xxxDxxxCxxBxxAxfxxfxRxfy或或的解集是那么不等式时当上的奇函数是定义在已知函数}25023|{.}250023|{.}023|{.}250|{.)(21)(,2)(,0,)(.11xxxDxxxCxxBxxAxfxxfxRxfy或或的解集是那么不等式时当上的奇函数是定义在已知函数Oxy2222212523