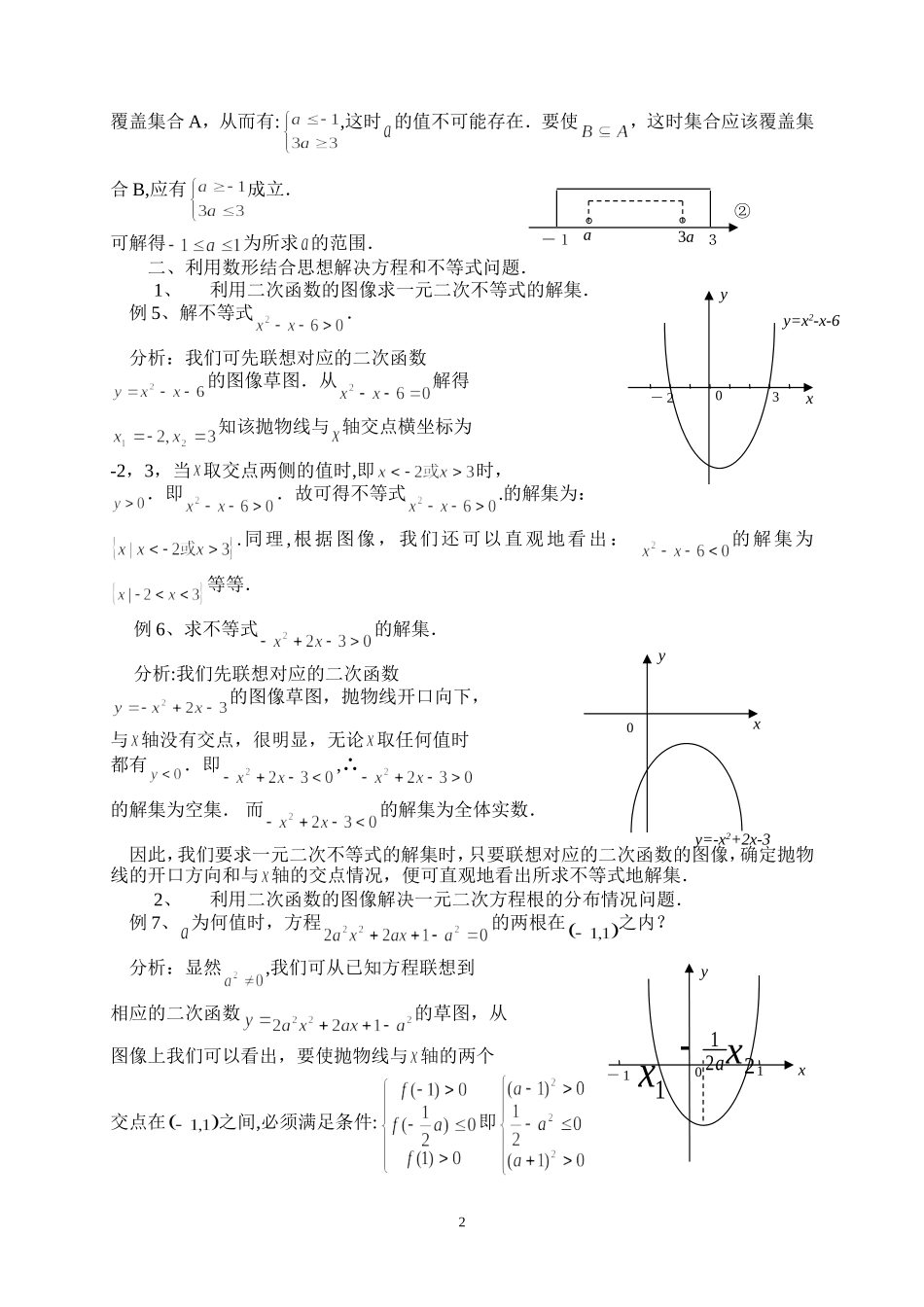
浅谈数形结合思想在高中数学中的几点应用 在解决数学问题时,将抽象的数学语言同直观的图形相结合,实现抽象的概念与具体形象的联系和转化,这就是数形结合的思想.在高中数学中,数形结合是一条重要的数学原则,主要体现在平面解析几何和立体几何中,在处理边角关系的问题中也有较多的应用.在解决集合问题、方程及不等式问题中,如果能注意数形结合的思想的应用,能使许多数学问题简单化.下面举一些例子作详细说明: 一、数形结合思想在解决集合问题中的应用. 1、利用韦恩图法解决集合之间的关系问题.一般用圆来表示集合,两圆相交则表示两集合有公共元素,两圆相离则表示两个集合没有公共元素.利用韦恩图法能直观地解答有关集合之间的关系的问题.如: 例 1、有 48 名学生,每人至少参加一个活动小组,参加数理化小组的人数分别为28,25,15,同时参加数理小组的 8 人,同时参加数化小组的 6 人,同时参加理化小组的 7人,问同时参加数理化小组的有多少人?分析:我们可用圆 A、B、C 分别表示参加数理化小组的人数(如右图),则三圆的公共部分正好表示同时参加数理化小组的人数.用 n 表示集合的元素,则有: 即:∴,即同时参加数理化小组的有 1 人. 例 2、设,已知 求 分析:如图,用长方形表示全集 I,用圆分别表示集合 A 和 B,用 n 表示集合的元素,则有:从韦恩图我们可以直观地看出:. 2、利用数轴解决集合的有关运算和集合的关系问题. 例 3、设 求 分析:分别先确定集合 A,B 的元素,,然后把它们分别在数轴上表示出来,从数轴上的重合和覆盖情况可直接写出答案: (公共部分) (整个数轴都被覆盖) (除去重合部分剩下的区域) (除去覆盖部分剩下的区域) 例 4、已知集合 ⑴ 若,求 的范围.⑵ 若,求 的范围. 分析:先在数轴上表示出集合 A 的范围,要使,由包含于的关系可知集合 B 应该1C (化)A (数)B (理)IA∩B3,5,72AB1,94,6,8。·- 4-20 1 243 。·。a3 a。-13①覆盖集合 A,从而有:,这时 的值不可能存在.要使,这时集合应该覆盖集合 B,应有成立.可解得为所求 的范围.二、利用数形结合思想解决方程和不等式问题.1、利用二次函数的图像求一元二次不等式的解集. 例 5、解不等式. 分析:我们可先联想对应的二次函数的图像草图.从解得知该抛物线与 轴交点横坐标为-2,3,当 取交点两侧的值时,即时,.即.故可得不等式.的解集为:....