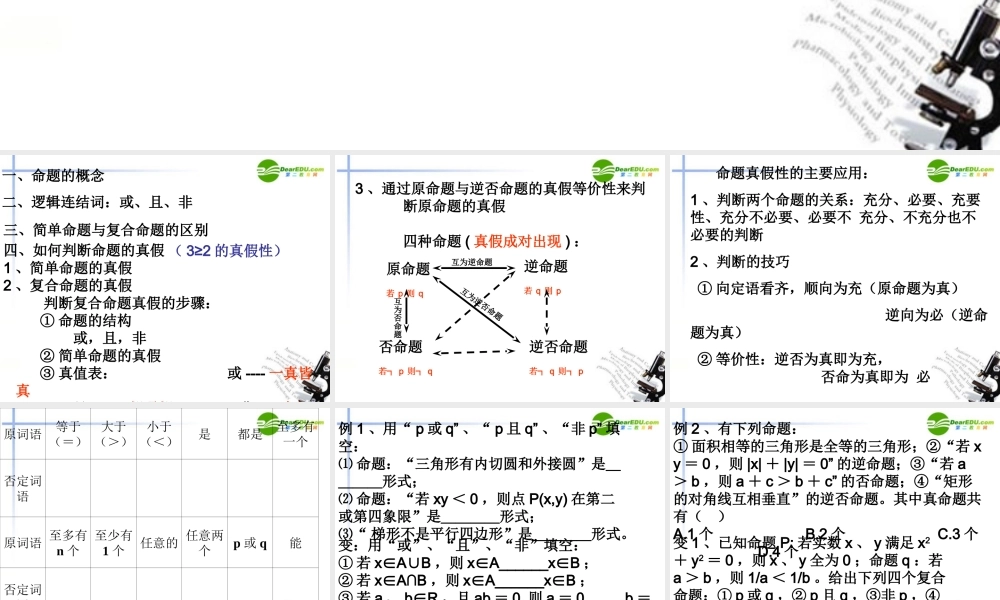
72 《逻辑联结词和四种命题》 四、如何判断命题的真假1 、简单命题的真假2 、复合命题的真假 判断复合命题真假的步骤: ① 命题的结构 或,且,非 ② 简单命题的真假 ③ 真值表: 或 ---- 一真皆真 且 ---- 一假通假 非 ---- 真假对立三、简单命题与复合命题的区别( 3≥2 的真假性)一、命题的概念二、逻辑连结词:或、且、非3 、通过原命题与逆否命题的真假等价性来判 断原命题的真假 四种命题 ( 真假成对出现 ) : 原命题若 p 则 q否命题若┐ p 则┐ q逆命题若 q 则 p逆否命题若┐ q 则┐ p互为逆命题互为否命题互为逆否命题 命题真假性的主要应用:1 、判断两个命题的关系:充分、必要、充要性、充分不必要、必要不 充分、不充分也不必要的判断2 、判断的技巧 ① 向定语看齐,顺向为充(原命题为真) 逆向为必(逆命题为真) ② 等价性:逆否为真即为充, 否命为真即为 必原词语等于(=)大于(>)小于(<)是都是至多有一个否定词语原词语 至多有n 个至少有1 个任意的 任意两个p 或 q能否定词语例 1 、用“ p 或 q” 、“ p 且 q” 、“非 p” 填空:⑴ 命题:“三角形有内切圆和外接圆”是____形式;⑵ 命题:“若 xy < 0 ,则点 P(x,y) 在第二或第四象限”是____形式;⑶“ 梯形不是平行四边形”是____形式。变:用“或”、“且”、“非”填空:① 若 xAB∈ ∪,则 xA______xB∈∈;② 若 xA∩B∈,则 xA______xB∈∈;③ 若 a 、 bR∈,且 ab = 0, 则 a = 0_____b =0 ;④ 若 a 、 bR∈,且 a2 + b2 = 0, 则 a = 0_____b = 0例 2 、有下列命题:① 面积相等的三角形是全等的三角形;②“若 xy = 0 ,则 |x| + |y| = 0” 的逆命题;③“若 a> b ,则 a + c > b + c” 的否命题;④“矩形的对角线互相垂直”的逆否命题。其中真命题共有( )A.1 个 B.2 个 C.3 个 D.4 个变 1 、已知命题 P: 若实数 x 、 y 满足 x2+ y2 = 0 ,则 x 、 y 全为 0 ;命题 q :若a > b ,则 1/a < 1/b 。给出下列四个复合命题:① p 或 q ,② p 且 q ,③非 p ,④非 q 。其中真命题的个数为( )A.1 B.2 C.3 D.4变 2 :由下列各组命题构成“ p 或 q” 、“ p 且 q” 、“非 p” 形式的复合命题中,“ p ...