高一数学 312两角和与差的正弦、余弦、正切公式课件(二) 课件VIP免费

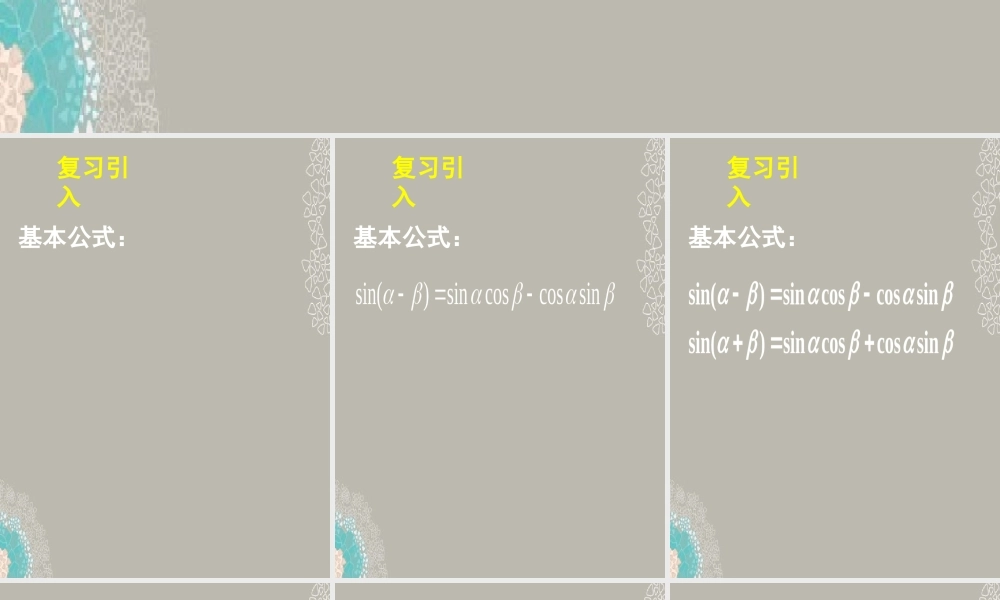
3.1.2 两角和与差的正弦、余弦、正切公式3.1.2 两角和与差的正弦、余弦、正切公式复习引入基本公式：复习引入基本公式：复习引入基本公式：复习引入基本公式：sinsincoscos)cos(复习引入基本公式：sinsincoscos)cos(sinsincoscos)cos(复习引入基本公式：tantan1tantan)tan(复习引入基本公式：tantan1tantan)tan(tantan1tantan)tan(练习教材 P.132 练习第 6 题 . 练习教材 P.132 练习第 6 题 . 思考：的类型？怎样求cossinba讲解范例：.sin6cos2xx 化简例 1..sin6cos2xx 化简讲解范例：例 1.思考：是怎么得到的？22讲解范例：归纳：)sin(cossin22babaabtan.,cos32sin2)(Rxxxxf已知函数讲解范例：例 2.(1) 求 f(x) 的最值；(2) 求 f(x) 的周期、单调性 .讲解范例：例 3. 已知 A 、 B 、 C 为△ ABC 的三内角，向量且.tan,3sincoscossin21)2(22的值求若CBBBB),sin,(cos),3,1(AAnm.1nm；求角A)1(练习：1. 教材 P.132 练习第 7 题 . 2. 在△ ABC 中， sinAsinB＜ cosAcosB ，则△ ABC 为 ( )A ．直角三角形 B ．钝角三角形 C ．锐角三角形 D ．等腰三角形练习：)(12sin12cos3.3的值为2D.2C.2B.0A.思考：.2sin,53)sin(,1312)cos(,432求已知课堂小结 掌握两角和与差的余弦、正弦和正切公式的应用及 asin ＋bcos类型的变换 .1. 阅读教材 P.128 到P.131; 2. 《习案》作业三十一的 第 1 、 2 、 3 题 .课后作业