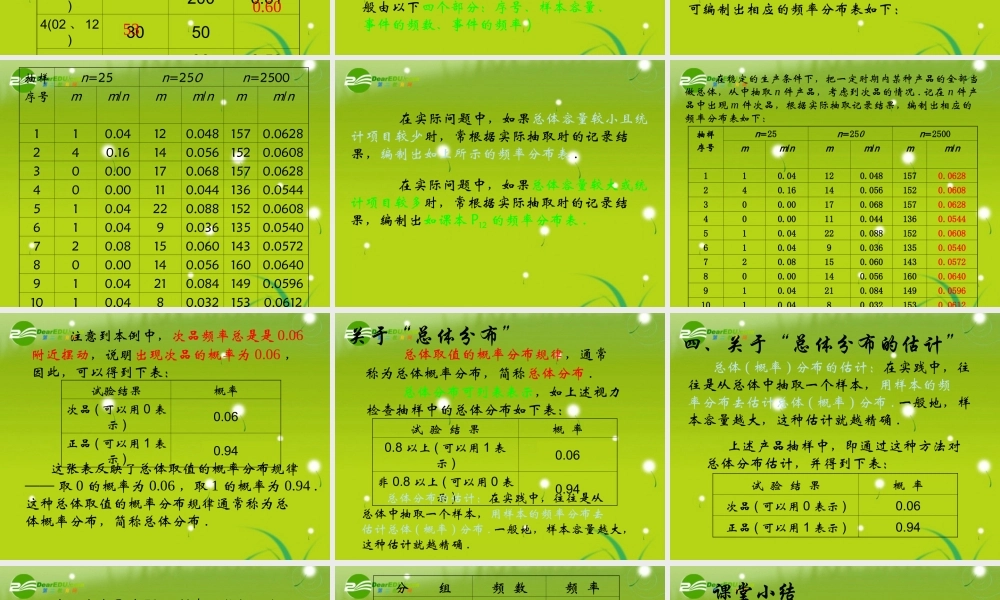
学习目标: 理解频数、频率、样本频率分布和总体分布等的概念; 掌握频数、样本容量和频率之间的等量关系; 会用样本频率分布估计总体分布 . 关于“频数、频率” 在一定条件下事件 A 在抽样中出现的次数叫做事件 A 出现的频数 . 事件 A 的频数在样本中所占的比率称为事件 A 抽样中出现的频率 .频率是不超过 1 的非负数有理数 .:友情提醒频数频率 = 样本容量 一个容量为 40 的样本,把它分成 6组,第一组到第四组的频数分别为 5,6,7,10. 第五组的频率是 0.2 ,则第六组的频数是 ,频率是 . 4 0.1例题 为了了解某校学生视力状况,该校校医在上学期每月抽检一次,并统计两眼视力均在 0.8 以上的学生人数 . 由于某种原因,记载表中某些数据丢失 ( 见下表 ) ,请同学们帮助复原此表 .例题抽样序号频 数样本容量频 率1(02 、 9)621002(02 、 10)480.603(02 、 11)2000.614(02 、 12)30505(03 、 1)900.590.620.608012253 关于“频率分布” 根据所抽取样本的大小,分别计算某一事件出现的频率,这些频率的分布规律 ( 取值状况 ) ,叫做样本的频率分布 . 通常将样本的容量、样本中出现该事件的频数以及计算所得的相应频率列在一张表中,叫做样本频率分布表 .( 一般由以下四个部分:序号、样本容量、事件的频数、事件的频率 )也就是说频率分布即频率规律 又如:在稳定的生产条件下,把一定时期内某种产品的全部当做总体,从中抽取 n 件 ( 即相当于做 n 次试验 ) ,考虑到次品的情况 . 记在 n件产品中抽取 m 件次品,则 m 叫次品出现的频数,次品数 m 占所抽的产品件数 n 的比率 称为产品抽验中次品出现的频率 . 显然 的取值范围是 中有理数组成的集合 .mnmn[0,1] 在上述产品抽样中,对应所抽取的不同样本 ( 容量为 n) ,根据实际抽取时的记录结果,可编制出相应的频率分布表如下: 抽样序号n=25n=250n=2500mm/nmm/nmm/n110.04120.0481570.0628240.16140.0561520.0608300.00170.0681570.0628400.00110.0441360.0544510.04220.0881520.0608610.0490.0361350.0540720.08150.0601430.0572800.00140.0561600.0640910.04210.0841490.05961010.0480.0321530.0612 在实际问题中,如果总体容量较小且统计项目较少时,常根据实际抽取时的记录结果,编制出如上所示的频率分布表 . 在实际问题中,如果总体容量较大或统计项目较多时,常根据实际抽取时的记录结...