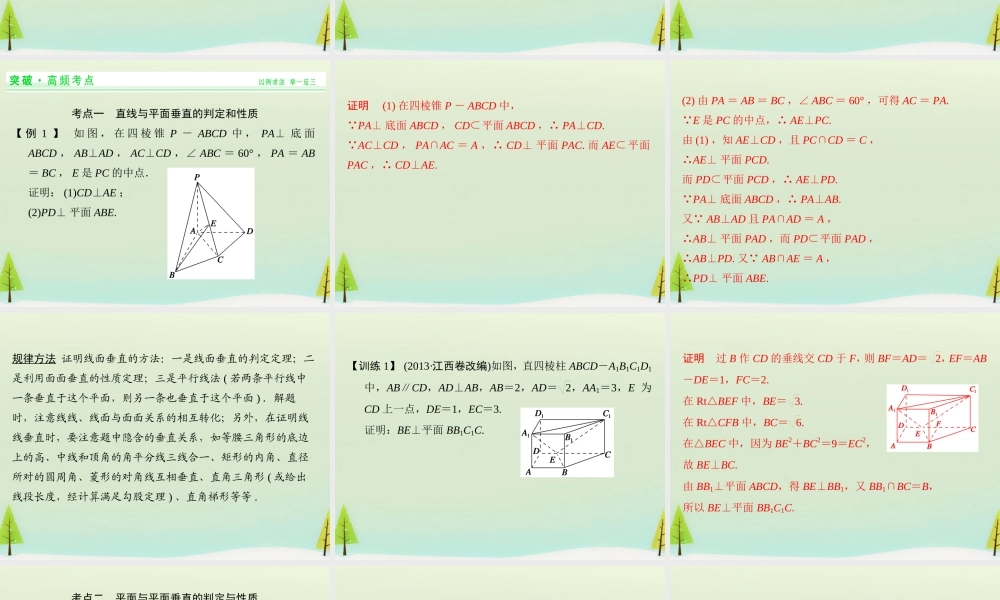
第 4 讲 直线、平面垂直的判定与性质知 识 梳 理1 .直线与平面垂直(1) 定义:若直线 l 与平面 α 内的 一条直线都垂直,则直线 l 与平面 α 垂直.(2) 判定定理:如果一条直线和一个平面内的两条 直线垂 直 , 那 么 这 条 直 线 垂 直 于 这 个 平 面 . 即 :a⊂α , b⊂α , l⊥a , l⊥b , a∩b = P⇒ .(3) 性质定理:垂直于同一个平面的两条直线 .即: a⊥α , b⊥α⇒ . 任意 相交l⊥α 平行a∥b 2 .平面与平面垂直(1) 定义:两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.(2) 判定定理:如果一个平面经过另一个平面的一条 ,那 么这两个平面互相垂直.即: a⊂α , a⊥β⇒ .(3) 性质定理:如果两个平面互相垂直,那么在一个平面内垂 直于它们 的直线垂直于另一个平面.即: , a⊂α , α∩β = b , a⊥b⇒ . 垂线α⊥β 交线a⊥β α⊥β3.直线与平面所成的角 (1)定义:平面的一条斜线和它在平面上的射影所成的锐角,叫做这条斜线和这个平面所成的角. (2)线面角 θ 的范围:θ∈0,π2 . 辨 析 感 悟1 .对线面垂直的理解(1) 直线 a , b , c ;若 a⊥b , b⊥c ,则 a∥c.(×)(2) 直线 l 与平面 α 内无数条直线都垂直,则 l⊥α.(×)(3)(2013· 浙江卷, 4C) 设 m , n 是两条不同的直线, α , β是两个不同的平面,若 m∥n , m⊥α ,则 n⊥α.(√)(4)(2013· 广东卷, 8D) 设 l 为直线, α , β 是两个不同的平面,若 α⊥β , l∥α ,则 l⊥β.(×)2 .对面面垂直的理解(5) 若两平面垂直,则其中一个平面内的任意一条直线垂直于另一个平面.(×)(6) 若平面 α 内的一条直线垂直于平面 β 内的无数条直线,则 α⊥β.(×)[ 感悟 · 提升 ]三个防范 一是注意在空间中垂直于同一直线的两条直线不一定平行,还有可能异面、相交等,如 (1) ;二是注意使用线面垂直的定义和线面垂直的判定定理,不要误解为“如果一条直线垂直于平面内的无数条直线,就垂直于这个平面”, 如 (2) ;三是注意对平面与平面垂直性质的理解,如 (5) .考点一 直线与平面垂直的判定和性质【 例 1 】 如 图 , 在 四 棱 锥 P - ABCD 中 , PA⊥ 底 面ABCD , AB⊥AD , AC⊥CD ,∠ ABC = 60° ,...