高考数学专题课件：正弦、余弦函数的图象 课件VIP免费

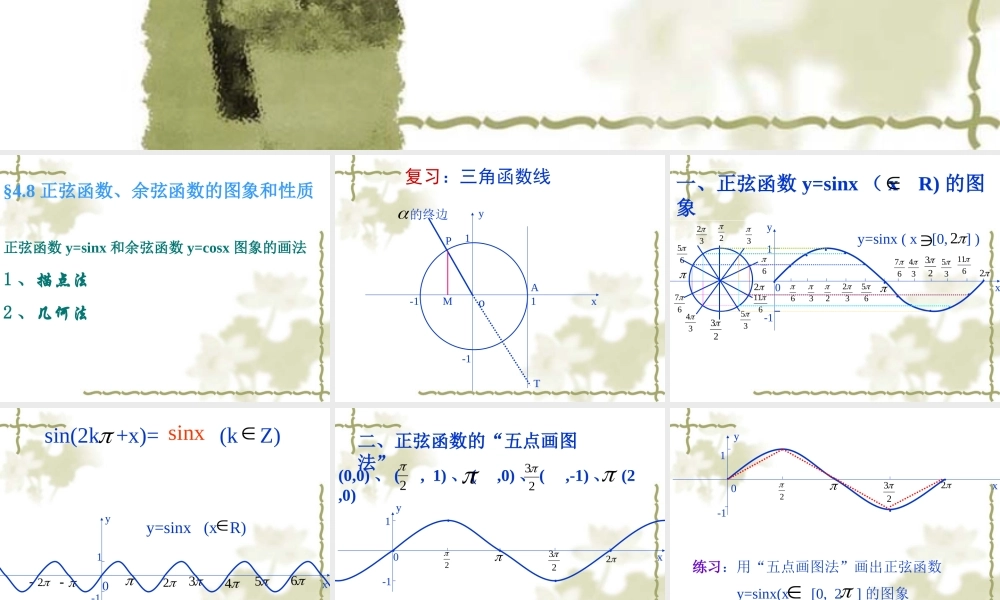
---- 正弦、余弦、正切函数图象三角函数图象普宁二中 蒋贤钦 §4.8 正弦函数、余弦函数的图象和性质正弦函数 y=sinx 和余弦函数 y=cosx 图象的画法1 、描点法2 、几何法 复习：三角函数线xyoPMT1A的终边-1-11 1-1022322656723352yx●●●一、正弦函数 y=sinx （ x R) 的图象y=sinx ( x [0, ] )2332346116633265●●●●●●●673435611●●● sin(2k +x)= (k Z)sinxxy23456021-1 y=sinx (x R)  二、正弦函数的“五点画图法”(0,0) 、 ( , 1) 、 ( ,0) 、 ( ,-1) 、 (2 ,0)2230xy1-1●●●●●2232 0xy1-1●●●●●2232练习：用“五点画图法”画出正弦函数 y=sinx(x [0, 2 ] 的图象 xy23456021-12 sin( x+ )=2三、余弦函数 y=cosx(x R) 的图象cosxy=sinx 的图象y=cosx 的图象223 余弦函数的“五点画图法”(0,1) 、 ( ,0) 、 ( ,-1) 、 ( ,0) 、 ( , 1)2232oxy2232●●●●●1-1 例 1 ：画出下列函数的简图(1)y=1+sinx ， x [0, ](2)y= - cosx ， x [0, ]22 解： (1) 按五个关键点列表xsinx1+sinx0 22320 1 0 -1 0 1 2 1 0 1oxy122232●●●●●y=1+sinx x [0, ]2 (2) 按五个关键点列表xcosx -cosx0 22321 0 -1 0 1 -1 0 1 0 -1oxy12232●●●●●y=-cosx x [0, ]2-1 思考：1 、函数 y=1+sinx 的图象与函数 y=sinx 的图象有什么关系？2 、函数 y=-cosx 的图象与函数 y=cosx 的图象有什么关系？ o-1122232y=sinx x [0, ]y=1+sinx x [0, ] 22yxyxo2232-11y=cosx x [0, ]y=-cosx x [0, ]22 例 2 用五点法作函数的简图 2cos(),[0,2 ]3yxx例 3 分别利用函数的图象和三角函数线两种方法，求满足下列条件的 x 的集合： 1(1)sin;2x 15(2)cos,(0).22xx 小结：1 ．正弦、余弦曲线 几何画法和五点法 2 ．注意与诱导公式，三角函数线的知识的联系 1 ．分别用单位圆中的三角函数线和五点法作出2 ．分别在 [-4,4] 内作出 y=sinx 和 y=cosx 的图象y=sinx 的图象 .3 ．用五点法作出 y=cosx,x[0,2] 的图象