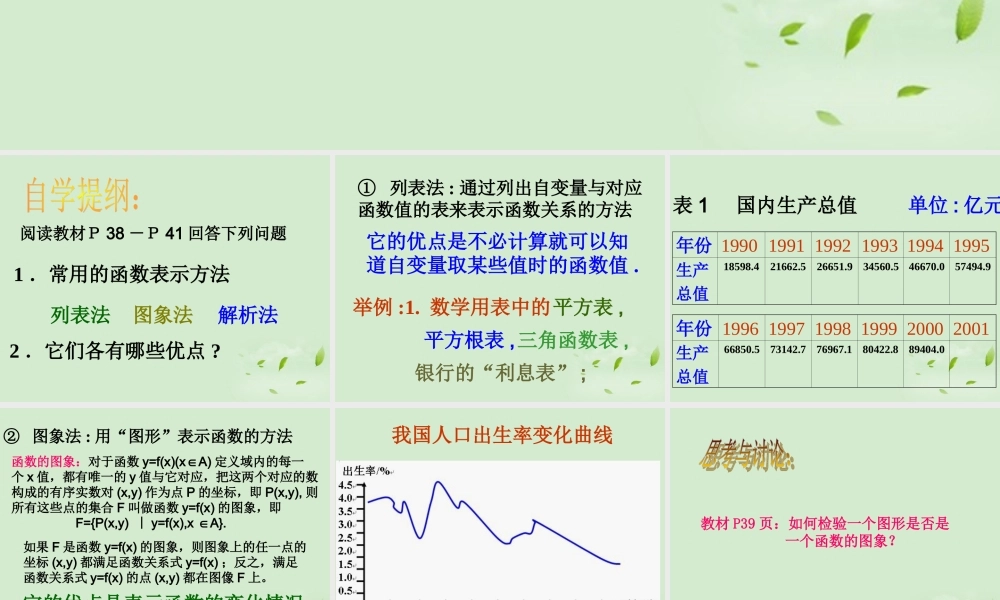
1 .常用的函数表示方法 图象法 2 .它们各有哪些优点 ? 解析法列表法阅读教材P 38 -P 41 回答下列问题 ① 列表法 : 通过列出自变量与对应函数值的表来表示函数关系的方法它的优点是不必计算就可以知道自变量取某些值时的函数值 .举例 :1. 数学用表中的平方表 ,银行的“利息表” ;平方根表 ,三角函数表 , 年份 1990 1991 1992 1993 1994 1995生产总值18598.421662.526651.934560.546670.057494.9年份 1996 1997 1998 1999 2000 2001生产总值66850.573142.776967.180422.889404.0表 1 国内生产总值 单位 : 亿元 ② 图象法 : 用“图形”表示函数的方法它的优点是表示函数的变化情况形象直观 .函数的图象:对于函数 y=f(x)(xA)∈定义域内的每一个 x 值,都有唯一的 y 值与它对应,把这两个对应的数构成的有序实数对 (x,y) 作为点 P 的坐标,即 P(x,y), 则所有这些点的集合 F 叫做函数 y=f(x) 的图象,即 F={P(x,y) ︱ y=f(x),x A}.∈如果 F 是函数 y=f(x) 的图象,则图象上的任一点的坐标 (x,y) 都满足函数关系式 y=f(x) ;反之,满足函数关系式 y=f(x) 的点 (x,y) 都在图像 F 上。 我国人口出生率变化曲线 教材 P39 页:如何检验一个图形是否是 一个函数的图象? ③ 解析法 : 用解析式表示两个变量 的函数关系 .它的优点是关系清楚 , 容易求数函值 , 便于研究函数的性质 .y=ax2+bx+c(a≠0),(2)x x-2等等 .y=举例 :s=60t2,r2,A=rl,S=2 1 、如何画出简单函数的图象?步骤有哪些?⑴ 列表; ⑵ 描点; ⑶ 连线1 、 x 的取值分布要恰当;2 、连线时要用光滑的曲线连接。 2 、高斯函数 y=[x] 是如何定义的?说出其图象特点。3 、画例 3 中函数的图象并说出其特点。函数的图象不仅可以是一段光滑 的曲线 , 还可以是若干条线段 , 甚 至 一些孤立的点 . 练习: 41 页 2加上范围求解析式 例 1(P54) 某种笔记本每个 5 元 , 买 x(x个笔记本的钱数记为{1,2,3,4,})y( 元 ). 试写出以 x 为自变量的函数 y的解析式 , 并画出这个函数的图象 .教科书 P54 - 例1 解 : 这个函数的定义域是集合 {1,2,3,4},函数解析式为5 ,({1,2,3,4}),yx x它的图象由 4 个孤立点组成 , 如图所示 , 这些点的坐标分别是 (1,5),(2,10),(3,15),(4,20). 例 2(P54) 国内投寄信函 ( 外埠 ), 邮资按下列...