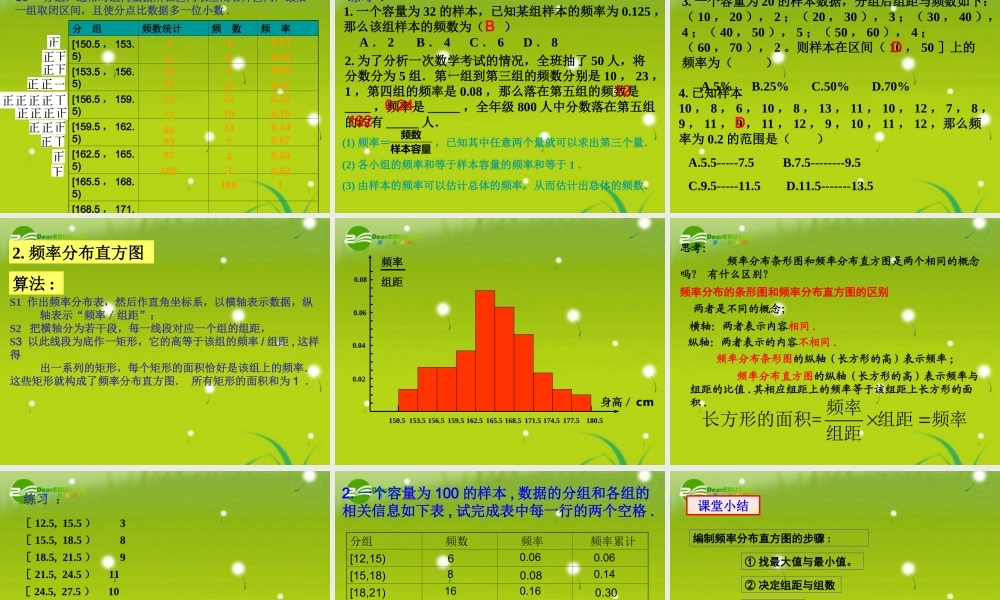
你身边的高考专家统计的基本思想方法: 用样本估计总体,即通常不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况 .统计的核心问题: 如何根据样本的情况对总体的情况作出一种推断 . 这里包括两类问题:一类是如何从总体中抽取样本 ? 另一类是如何根据对样本的整理、计算、分析 , 对总体的情况作出推断 . 用样本的有关情况去估计总体的相应情况 ,这种估计大体分为两类,一类是用样本频率分布估计总体分布,一类是用样本的某种数字特征(例如平均数、方差等)去估计总体的相应数字特征。 整体介绍: 国际奥委会 2003 年 6 月 29 日决定, 2008 年北京奥运会举办的日期比原定日期推迟两周,改在 8 月 8 日至 8 月 24 日举行.原因是 7 月末 8 月初北京地区得气温高于 8 月中下旬. 下表是随机抽取的近年来北京地区 7 月 25 日至 8 月 24 日的日最高气温,得到如下样本 ( 单位:ºC)7 月 25日至 8 月10 日41.937.535.735.437.238.134.733.733.332.534.633.030.831.028.631.528.88 月 8 日至 8 月24 日28.631.528.833.232.530.330.229.833.132.829.425.624.730.030.129.530.3怎样通过上表中的数据,分析比较两时间段的高温(≥ 33℃ )状况呢?问题引入:知识新授:1. 频数与频率 频数是指一组数据中,某范围内的数据出现的次数;把频数除以数据的总个数,就得到频率 .2. 频率分布表 当总体很大或不便于获得时,可以用样本的频率分布估计总体的频率分布 . 我们把反映总体频率分布的表格称为频率分布表 .说明:样本频率分布与总体频率分布 有什么关系?通过样本的频数分布、频率分布可以估计总体的频率分布 .7 月 25 日至 8 月 10日41.9 37.5 35.7 35.4 37.2 38.1 34.7 33.7 33.332.5 34.6 33.0 30.8 31.0 28.6 31.5 28.88 月 8 日至 8 月 24日28.6 31.5 28.8 33.2 32.5 30.3 30.2 29.8 33.132.8 29.4 25.6 24.7 30.0 30.1 29.5 30.3时间总天数高温天数频率7 月 25 日至 8 月10 日17110.6478 月 8 日至 8 月24 日1720.118频率分布表 :3. 频率分布条形图时间总天数高温天数频率7 月 25 日至 8 月10 日17110.6478 月 8 日至 8 月24 日1720.118① 各长方形长条的宽度要相同 .② 相邻长条的间距要适当 .③ 长方形长条的高度表示取各值的频率 .0.10.20.30.40.50.60...